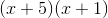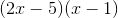All Algebra 1 Resources
Example Questions
Example Question #21 : How To Factor A Trinomial
Factor the following trinomial:
To factor the trinomial, its general form given by 


For our trinomial, 





Using the two factors, we can rewrite the term 
Now, we must factor by grouping, which means we group the first two terms, and the last two terms, and factor them:
Note that after we factored the two groups of terms, what remained inside the parentheses is identical for the two groups.
Simplifying further, we get

Example Question #22 : Trinomials
Which of the following is a perfect square trinomial?
A perfect square trinomial takes the form

where
Since 


This makes 
Example Question #1 : Simplifying Polynomials
Multiply:
Set up this problem vertically like you would a normal multiplication problem without variables. Then, multiply the 

Then combine the two, which yields:
Example Question #1 : Expanding Expressions And Foil
Multiply the expressions:
You can look at this as the sum of two expressions multiplied by the difference of the same two expressions. Use the pattern

where 


To find 

where 

Substituting above, the final answer is 
Example Question #1 : How To Multiply Trinomials
Evaluate the following:
When multiplying these two trinomials, you'll need to use a modified form of FOIL, by which every term in the first trinomial gets multiplied by every term in the second trinomial. One way to do this is to use the grid method.
You can also solve it piece by piece the way it is set up. First, multiply each of the three terms in the first trinomail by 


Finally, you can combine like terms after this multiplication to get your final simplified answer:
Example Question #4 : Simplifying And Expanding Quadratics
Evaluate the following:
When multiplying this trinomial by this binomial, you'll need to use a modified form of FOIL, by which every term in the binomial gets multiplied by every term in the trinomial. One way to do this is to use the grid method.
You can also solve it piece-by-piece the way it is set up. First, multiply each of the three terms in the trinomail by 

Finally, you can combine like terms after this multiplication to get your final simplified answer:
Example Question #23 : Trinomials
Multiply:
Solving this is just like using FOIL on binomials, except we have nine calculations to perform instead of four (since that's the result of a 3x3 combination!):
First, calculate the combinations of the first term on the left:
Next, calculate the combinations of the middle term on the left:
Next, calculate the combinations of the third term on the left:
Lastly, combine the terms with compatible variables and exponents:
Thus, our answer is 
Example Question #24 : Trinomials
Multiply:
To solve this problem, first FOIL the binomial.
FOIL stands for the multiplication between the first terms, outer terms, inner terms, and then the last terms.
Now, distribute the trinomials. Start with the first term on the left:
Now the middle term on the left:
Now, the third term on the left:
Combine all compatible terms:
Thus, 
Example Question #27 : Trinomials
Multiply:
The easy way to perform this calculation (without using Pascal's Triangle) is to find 
So, our problem becomes
Start by distributing the first term on the left:
Now distribute the second term on the left:
Now distribute the third term on the left:
Now, combine the compatible terms:
Thus, our answer is 
Example Question #28 : Trinomials
Expand and simplify the expression:
We are asked to expand and simplify the expression: 
This question is going to require knowledge of exponent rules and FOIL methods.
The first step is to create an inverse reciprocal of a negative exponent.
Now, we can expand the expression by removing the exponent in the denominator.
Use the FOIL method to first multiply 

You'll find it creates 

Be careful with exponents and coefficients!
Combine like terms to find the simplified answer.
All Algebra 1 Resources