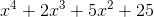The degree of a polynomial is determined by the term with the highest degree. In this case, the first term, , has the highest degree, . The degree of a term is calculated by adding the exponents of each variable in the term.

The degree of a polynomial is determined by the term with the highest degree. In this case, the first term, , has the highest degree, . The degree of a term is calculated by adding the exponents of each variable in the term.

The degree of a polynomial is the highest exponent of the terms.

Degree 0 – constant

Degree 1 – linear

Degree 2 – quadratic

Degree 3 – cubic

Degree 4 – quartic

Multiply out the equation:

(y + 2)(y + 4)(y + 1) = z

(y2 + 2y + 4y + 8)(y + 1) = z

y3 + 2y2 + 4y2 + 8y + y2 + 2y + 4y + 8 = z

The highest exponent is y3;therefore the equation is a degree 3 cubic.

The degree of a polynomial is the highest exponent of the terms.

Degree 0 – constant

Degree 1 – linear

Degree 2 – quadratic

Degree 3 – cubic

Degree 4 – quartic

Multiply out the equation:

(y + 2)(y + 4)(y + 1) = z

(y2 + 2y + 4y + 8)(y + 1) = z

y3 + 2y2 + 4y2 + 8y + y2 + 2y + 4y + 8 = z

The highest exponent is y3;therefore the equation is a degree 3 cubic.

The question provides two positive whole numbers that are each multiples of 6 and also 6 numbers apart. This may be translated into variables, where the first number may be represented by "x" and the second number may be represented as "x+6" given that it is 6 numbers greater than x.

The problem provides the information that the product of these two numbers is 72. Using the new definitions for the numbers, this may be represented as:

(x)(x+6) = 72

This provides an equation that multiplies two polynomials (one with one term, which is a monomial and one with two terms, which is a binomial) and an ability to solve for what x (the first of the two numbers) may be.

Using FOIL, the result is . This may be rewritten as , which will provide the value of x after factoring.

, where (-6)(12) will provide the product of -72 and the sum of 12 and -6 will yield 6. The results indicate x as having two possible solutions: x=6 and x=-12. Returning back to the question, the goal is to find two positive numbers. This means that x=-12 is not a viable solution and that x=6 is. Now, revisiting the terms used to redefine the two numbers \[x and x+6\], x has been calculated. After substituting in the x value for the second term, the second number is 12 (6+6=12).

The final step of the problem is to solve for the sum of these two numbers:
6+12=18

The question provides two positive whole numbers that are each multiples of 6 and also 6 numbers apart. This may be translated into variables, where the first number may be represented by "x" and the second number may be represented as "x+6" given that it is 6 numbers greater than x.

The problem provides the information that the product of these two numbers is 72. Using the new definitions for the numbers, this may be represented as:

(x)(x+6) = 72

This provides an equation that multiplies two polynomials (one with one term, which is a monomial and one with two terms, which is a binomial) and an ability to solve for what x (the first of the two numbers) may be.

Using FOIL, the result is . This may be rewritten as , which will provide the value of x after factoring.

, where (-6)(12) will provide the product of -72 and the sum of 12 and -6 will yield 6. The results indicate x as having two possible solutions: x=6 and x=-12. Returning back to the question, the goal is to find two positive numbers. This means that x=-12 is not a viable solution and that x=6 is. Now, revisiting the terms used to redefine the two numbers \[x and x+6\], x has been calculated. After substituting in the x value for the second term, the second number is 12 (6+6=12).

The final step of the problem is to solve for the sum of these two numbers:
6+12=18

In adding to both sides:

. . .and adding to both sides:

. . .the variables are isolated to become:

After dividing both sides by , the equation becomes:

Expand:

Step 1: Use the distributive property

Step 2: Combine like terms

In adding to both sides:

. . .and adding to both sides:

. . .the variables are isolated to become:

After dividing both sides by , the equation becomes:

1. Factor the numerator:

2. Factor the denominator:

3. Divide the factored numerator by the factored denominator:

You can cancel out the from both the numerator and the denominator, leaving you with: