All ACT Math Resources
Example Questions
Example Question #1 : Polynomial Operations
What type of equation is the following?
(y + 2)(y + 4)(y + 1) = z
quadratic
cubic
constant
linear
quartic
cubic
The degree of a polynomial is the highest exponent of the terms.
Degree 0 – constant
Degree 1 – linear
Degree 2 – quadratic
Degree 3 – cubic
Degree 4 – quartic
Multiply out the equation:
(y + 2)(y + 4)(y + 1) = z
(y2 + 2y + 4y + 8)(y + 1) = z
y3 + 2y2 + 4y2 + 8y + y2 + 2y + 4y + 8 = z
The highest exponent is y3;therefore the equation is a degree 3 cubic.
Example Question #1 : Polynomials
Find the degree of the polynomial:
The degree of a polynomial is determined by the term with the highest degree. In this case that is 

Example Question #1 : Polynomial Operations
What is the degree of the following polynomial?
The degree of a polynomial is determined by the term with the highest degree. In this case, the first term, 

Example Question #2 : Polynomials
What is 
1. Factor the numerator:
2. Factor the denominator:
3. Divide the factored numerator by the factored denominator:
You can cancel out the 
Example Question #1 : Polynomials
Simplify:
In order to divide these polynomials, you need to first factor them.
and
Now, the expression becomes
so,
Example Question #2 : How To Divide Polynomials
Simplify the following division of polynomials:
It cannot be simplified any further.
The leading term of the numerator is one exponent higher than the leading term of the denominator. Thus, we know the result of the division is going to be somewhere close to 
The first term is easily seen to be 

and combining these, we get our final answer,
Example Question #22 : Variables
Expand:
Expand:
Step 1: Use the distributive property
Step 2: Combine like terms
Example Question #1 : How To Multiply Polynomials
Two positive consecutive whole numbers that are even are both multiples of 

The question provides two positive whole numbers that are each multiples of 6 and also 6 numbers apart. This may be translated into variables, where the first number may be represented by "x" and the second number may be represented as "x+6" given that it is 6 numbers greater than x.
The problem provides the information that the product of these two numbers is 72. Using the new definitions for the numbers, this may be represented as:
(x)(x+6) = 72
This provides an equation that multiplies two polynomials (one with one term, which is a monomial and one with two terms, which is a binomial) and an ability to solve for what x (the first of the two numbers) may be.
Using FOIL, the result is 


The final step of the problem is to solve for the sum of these two numbers:
6+12=18
Example Question #8 : Polynomial Operations
Multiply these polynomials out and expand.
The proper way to multiply polynomials is to essentially apply the distributive property continually.
So 
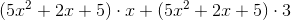
Then, simply group together like terms to get the final answer:
Example Question #1 : How To Subtract Polynomials
Simplify:
When subtracting polynomials, it's helpful to remember that the "minus sign" gets distributed. It's as if the two polynomials are being added and a -1 is in front of the second polynomial.
This -1 will get multiplied to all the terms in the second polynomial that is being subtracted from the first, so it becomes 
From here, in order to simplify, because there's no equal sign, it can be deduced that we are not working toward a solution for x. The original problem is presented as an expression so an expression as an answer will be expected. In order to work towards a final simplified expression, like terms must be collected. This will provide the final answer.

Certified Tutor
Certified Tutor
All ACT Math Resources