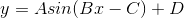Phase Shifts
Help Questions
Trigonometry › Phase Shifts
Which of the following is the correct definition of a phase shift?
A measure of the length of a function between vertical asymptotes
The distance a function is shifted diagonally from the general position
The distance a function is shifted horizontally from the general position
The distance a function is shifted vertically from the general position
Explanation
Take the function 

If we were to change the function to 


Our new graph 
Consider the function 
Explanation
The general form for the secant transformation equation is 





True or False: The function 

True
False
Explanation
The form of the general cosecant function is 




Which of the following is the phase shift of the function 
Explanation
The general form of the cotangent function is 


From this we see that 
True or False: If the function 

True
False
Which of the following is the graph of 





Explanation
Start this problem by graphing the function of tangent.

Now we need to shift this graph 

This gives us our answer

Identify the phase shift of the following equation.
Explanation
If we use the standard form of a sine function
the phase shift can be calculated by 
Which of the following is equivalent to
Explanation
The first zero can be found by plugging 3π/2 for x, and noting that it is a double period function, the zeros are every π/2, count three back and there is a zero at zero, going down.
A more succinct form for this answer is 
The first positive peak is at π/4 at -1, so the cosine function will be shifted π/4 to the right and multiplied by -1. The period and amplitude still 2, so the answer becomes 
To check, plug in π/4 for x and it will come out to -2.










 has a period of
has a period of  , meaning it repeats itself every
, meaning it repeats itself every  units. So if
units. So if  has a phase shift of any multiple of
has a phase shift of any multiple of  and in purple is the graph of
and in purple is the graph of  .
.