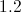All SSAT Upper Level Math Resources
Example Questions
Example Question #1 : How To Find The Reciprocal Of A Fraction
Give the reciprocal of 0.8.
The reciprocal of a number is the quotient of 1 and that number. Divide 1 by 0.8 by moving the decimal point to the right in each number one place:
Example Question #2 : How To Find The Reciprocal Of A Fraction
Give the reciprocal of 0.75.
The reciprocal of a number is the quotient of 1 and the number.
Divide 1 by 0.75 by moving the decimal point to the right in each number two places:
Example Question #1321 : Ssat Upper Level Quantitative (Math)
Add the reciprocals of 0.3 and 0.7. What is their sum?
The correct answer is not among the other responses.




Add them:

Example Question #3 : How To Find The Reciprocal Of A Fraction
Subtract the reciprocal of 1.5 from the reciprocal of 0.125. What is the result?
The correct answer is not among the other responses.



The requested difference is
Example Question #1323 : Ssat Upper Level Quantitative (Math)
Let 



Since 
Therefore, 
Example Question #5 : How To Find The Reciprocal Of A Fraction
Let 



If 100 is divided by 177, the decimal equivalent is seen to be 

Example Question #5 : Reciprocals
Subtract the reciprocal of 11 from the reciprocal of 13. What is the result?
The reciprocals of 11 and 13 are, respectively, 

This answer is not among the given choices.
Example Question #4 : How To Find The Reciprocal Of A Fraction
Add the reciprocals of 


The reciprocals of 4, 6, and 8 are, respectively, 
First we find the least common denominator between all three fractions.
All SSAT Upper Level Math Resources