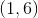All SAT Math Resources
Example Questions
Example Question #651 : Sat Mathematics
On the coordinate plane, a triangle has its vertices at the points with coordinates 


The referenced figure is below.

The triangle formed is a right triangle whose hypotenuse is the segment with the endpoints 

can be applied, setting 
The midpoint of the hypotenuse, and, consequently, the center of the circumscribed circle, is the point with coordinates 
Example Question #652 : Sat Mathematics
On the coordinate plane, 




















Which of these statements is true of 





















Another way of viewing this problem is to note that the three given vertices form a triangle 






Example Question #655 : Sat Mathematics

Figure NOT drawn to scale.
On the coordinate axes shown above, the shaded triangle has area 40.
Evaluate 
The length of the horizontal leg of the triangle is the distance from the origin 

The area of a right triangle is half the product of the lengths of its legs 




Therefore, the length of the vertical leg is 10, and, since the 




so, setting 

Set 


the line has equation
The 



Example Question #2 : New Sat Math Calculator
Mrs. Smith's 8th grade class has a weekly quiz. The graph below depicts the number of questions students got incorrect on their quiz and their corresponding quiz grade. Examining the graph, what type of correlation if any, exists?

The graph depicts a constant correlation.
More information is needed.
The graph depicts a positive correlation.
The graph depicts a negative correlation.
The graph depicts no correlation.
The graph depicts a negative correlation.
Mrs. Smith's 8th grade class had a quiz last week. The graph below depicts the number of questions students got incorrect on their quiz and their corresponding quiz grade. In other words, the graph in this particular question is a dot plot and the question asks to find a correlation if one exists.
Recall that a correlation is a trend seen in the data. Graphically, trends can be either:
I. Positive
II. Negative
III. Constant
IV. No trend
For a trend to be positive the x and y variable both increase. A trend is negative when the y variable (dependent variable) decreases as the x variable (independent variable) increases. A constant trend occurs when the y variable stays the same as the x variable increases. No trend exists when the data appears to be scattered with no association between the x and y variables.

Examining the graph given it is seen that the x variable is the number of questions missed and the y variable is the overall score on the quiz. It is seen that as the number of questions missed increases, the overall score on the quiz decreases. This describes a negative trend.
In other words, the graph depicts a negative correlation.
Example Question #1 : How To Graph A Point
Given the graph of record sales, what fraction of records were sold in 2004 to 2010?

Given the graph of record sales, to find the fraction of records that were sold in 2004 to 2010 first identify the record sales in 2004 and the record sales in 2010.
Examining the graph,
Record sales in 2004:14 million
Record sales in 2010: 13 million
From here, to find the fraction of records sold during this time period, use the following formula.
Example Question #2 : How To Graph An Ordered Pair
Which of the following coordinate pairs is farthest from the origin?
Using the distance formula, calculate the distance from each of these points to the origin, (0, 0). While each answer choice has coordinates that add up to seven, (-1, 8) is the coordinate pair that produces the largest distance, namely 
Example Question #1 : How To Graph An Ordered Pair
On the coordinate plane, the point with coordinates 
Quadrant II
None of these
Quadrant IV
Quadrant III
Quadrant I
Quadrant II
On the coordinate plane, a point with a negative 
Example Question #1 : How To Graph A Line
A line graphed on the coordinate plane below. 
Give the equation of the line in slope intercept form.
The slope of the line is 

The equation of the line is 
Example Question #2 : How To Graph A Line

Give the equation of the curve.
None of the other answers
 This is the parent graph of
This is the parent graph of 

Example Question #666 : Sat Mathematics
Give the area of the triangle on the coordinate plane that is bounded by the lines of the equations 


It is necessary to find the coordinates of the vertices of the triangle, each of which is the intersection of two of the three lines.
The intersection of the lines of the equations 





The intersection of the lines of the equations 




This point of intersection is 
The intersection of the lines of the equations 




Since 


The lines in question are graphed below, and the triangle they bound is shaded:

We can take the horizontal side as the base of the triangle; its length is the difference of the 
The height is the vertical distance from this side to the opposite side, which is the difference of the 
The area is half their product:
All SAT Math Resources