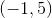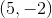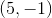All SAT II Math I Resources
Example Questions
Example Question #143 : Geometry
Reflect the point 

Reflecting the point across the vertical line 
The point after this reflection is:
Rotating this point across the origin will swap the x and y-values.
The new point is:
Example Question #1 : How To Find Transformation For An Analytic Geometry Equation
Let 



When a function 



Our final answer is therefore
Example Question #2 : How To Find Transformation For An Analytic Geometry Equation
Let 



When a function 





Our final answer is therefore
Example Question #211 : Coordinate Geometry
Let 





When a function 








Now we can apply the horizontal transformation by replacing all 

We then multiply this out to obtain:
Our final answer is therefore
Example Question #1 : Transformation
How is 

The graph of 

The graph of 

The slope of 

The graph of 

The slope of 

The standard form of a linear equation is 






Example Question #2 : Transformations
Given 

Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is 








Example Question #3 : Transformations
Given 

Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is 








Example Question #1 : Transformations
Given 

Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is 




First, multiply the slope by three.
Add one to the independent variable.
Subtract three from the constant term.







Example Question #1 : How To Find Transformation For An Analytic Geometry Equation
If this is a sine graph, what is the phase displacement?
0
π
2π
(1/2)π
4π
0
The phase displacement is the shift from the center of the graph. Since this is a sine graph and the sin(0) = 0, this is in phase.
Example Question #901 : Act Math
If this is a cosine graph, what is the phase displacement?
π
4π
0
(1/2)π
2π
π
The phase displacement is the shift of the graph. Since cos(0) = 1, the phase shift is π because the graph is at its high point then.
Certified Tutor
All SAT II Math I Resources