All SAT II Math I Resources
Example Questions
Example Question #1 : Graphing Other Functions
Simplify the following expression:
To simplify, we must first simplify the absolute values.
Now, combine like terms:
Example Question #1 : Graphing Polynomial Functions
Where does 

5
-7
7
-3
3
7




Example Question #142 : Functions And Graphs

Which of the following is an equation for the above parabola?
The zeros of the parabola are at 


each of their signs is reversed to end up with the correct sign in the answer. The coefficient can be found by plugging in any easily-identifiable, non-zero point to the above formula. For example, we can plug in 

Example Question #2 : Graphing Other Functions
Which equation best represents the following graph?
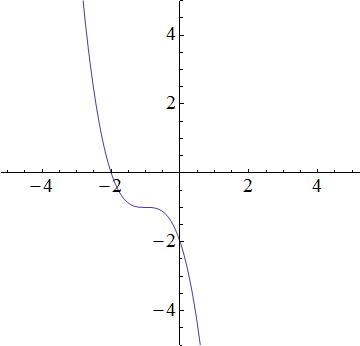
None of these
We have the following answer choices.
The first equation is a cubic function, which produces a function similar to the graph. The second equation is quadratic and thus, a parabola. The graph does not look like a prabola, so the 2nd equation will be incorrect. The third equation describes a line, but the graph is not linear; the third equation is incorrect. The fourth equation is incorrect because it is an exponential, and the graph is not an exponential. So that leaves the first equation as the best possible choice.
Example Question #1 : Graphing Polynomial Functions
Which of the graphs best represents the following function?
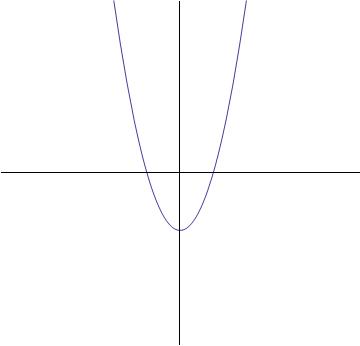



None of these

The highest exponent of the variable term is two (
The graph below will be the answer, as it shows a parabolic curve.

Example Question #1 : Graphing Polynomial Functions
Which of the following is a graph for the following equation:
Cannot be determined

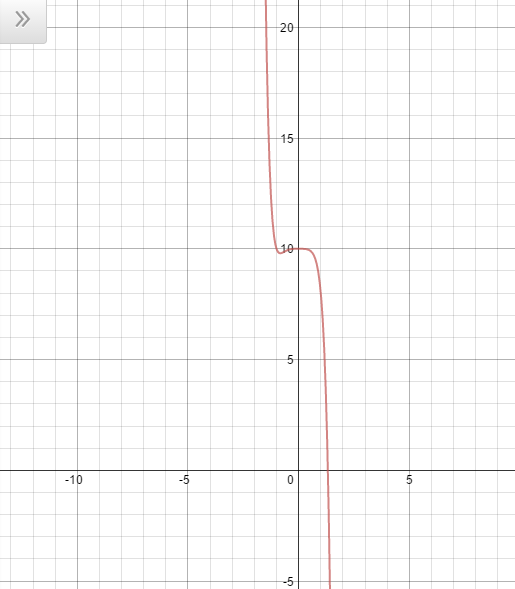



The way to figure out this problem is by understanding behavior of polynomials.
The sign that occurs before the 

Example Question #22 : Graphing Functions
Define a function 



Which of the following statements is correct about 
Define 


By the Intermediate Value Theorem (IVT), if 





Evaluate 
Only in the case of 





All SAT II Math I Resources









































