All PSAT Math Resources
Example Questions
Example Question #491 : Psat Mathematics

Example Question #491 : Psat Mathematics
Kathy and Jill are travelling from their home to the same destination. Kathy travels due east and then after travelling 6 miles turns and travels 8 miles due north. Jill travels directly from her home to the destination. How miles does Jill travel?
Kathy's path traces the outline of a right triangle with legs of 6 and 8. By using the Pythagorean Theorem


Example Question #102 : Geometry
Example Question #141 : Geometry
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
6√2
15
2√5
11
10√2
10√2
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
Example Question #52 : Triangles
Jim leaves his home and walks 10 minutes due west and 5 minutes due south. If Jim could walk a straight line from his current position back to his house, how far, in minutes, is Jim from home?
√5
6√6
√10
5√5
5√5
By using Pythagorean Theorem, we can solve for the distance “as the crow flies” from Jim to his home:
102 + 52 = x2
100 + 25 = x2
√125 = x, but we still need to factor the square root
√125 = √25*5, and since the √25 = 5, we can move that outside of the radical, so
5√5= x
Example Question #51 : Right Triangles
A square enclosure has a total area of 3,600 square feet. What is the length, in feet, of a diagonal across the field rounded to the nearest whole number?
100
95
85
75
60
85
In order to find the length of the diagonal accross a square, we must first find the lengths of the individual sides.
The area of a square is found by multiply the lengths of 2 sides of a square by itself.
So, the square root of 3,600 comes out to 60 ft.
The diagonal of a square can be found by treating it like a right triangle, and so, we can use the pythagorean theorem for a right triangle.
602 + 602 = C2
the square root of 7,200 is 84.8, which can be rounded to 85
Example Question #1251 : Basic Geometry
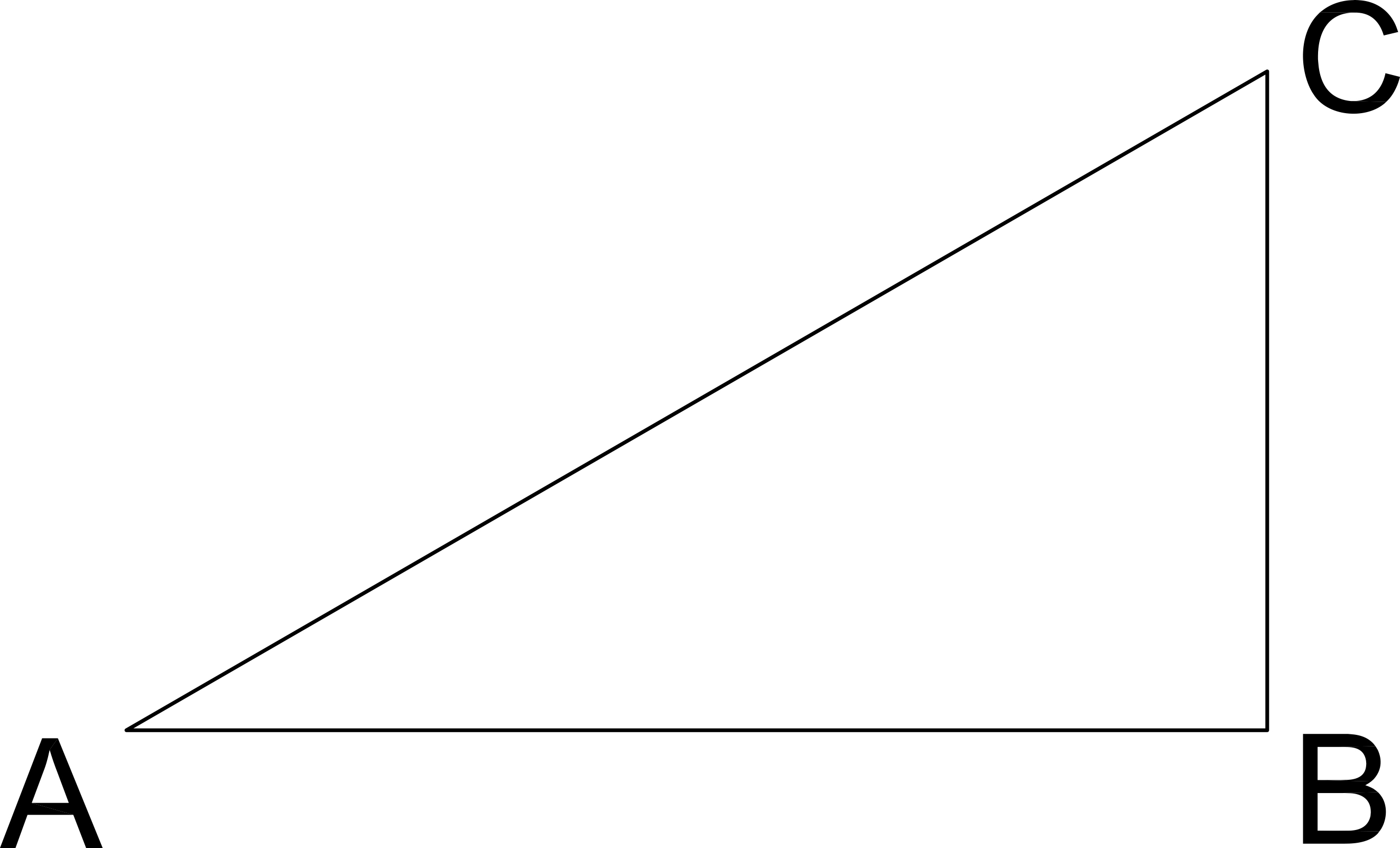
If the length of CB is 6 and the angle C measures 45º, what is the length of AC in the given right triangle?
72
6√2
12√2
6
9
6√2
Pythagorean Theorum
AB2 + BC2 = AC2
If C is 45º then A is 45º, therefore AB = BC
AB2 + BC2 = AC2
62 + 62 = AC2
2*62 = AC2
AC = √(2*62) = 6√2
Example Question #32 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
You leave on a road trip driving due North from Savannah, Georgia, at 8am. You drive for 5 hours at 60mph and then head due East for 2 hours at 50mph. After those 7 hours, how far are you Northeast from Savannah as the crow flies (in miles)?
Distance = hours * mph
North Distance = 5 hours * 60 mph = 300 miles
East Distance = 2 hours * 50 mph = 100 miles
Use Pythagorean Theorem to determine Northeast Distance
3002 + 1002 =NE2
90000 + 10000 = 100000 = NE2
NE = √100000
Example Question #33 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
A square garden has an area of 49 ft2. To the nearest foot, what is the diagonal distance across the garden?
8
7
11
10
9
10
Since the garden is square, the two sides are equal to the square root of the area, making each side 7 feet. Then, using the Pythagorean Theorem, set up the equation 72 + 72 = the length of the diagonal squared. The length of the diagonal is the square root of 98, which is closest to 10.
Example Question #1252 : Basic Geometry
A man at the top of a lighthouse is watching birds through a telescope. He spots a pelican 5 miles due north of the lighthouse. The pelican flies due west for 12 miles before resting on a buoy. What is the distance, in miles, from the pelican's current resting spot to the lighthouse?
We look at the 3 points of interest: the lighthouse, where the pelican started, and where the pelican ended. We can see that if we connect these 3 points with lines, they form a right triangle. (From due north, flying exactly west creates a 90 degree angle.) The three sides of the triangle are 5 miles, 13 miles and an unknown distance. Using the Pythagorean Theorem we get:
Certified Tutor
All PSAT Math Resources








































