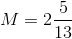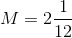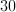Triangles
Help Questions
PSAT Math › Triangles

In the figure above, 



Explanation
Assigning the length of ED the value of x, the value of AE will be 3_x_. That makes the entire side AD equal to 4_x_. Since the figure is a square, all four sides will be equal to 4_x_. Also, since the figure is a square, then angle A of triangle ABE is a right angle. That gives triangle ABE sides of 3_x_, 4_x_ and 10. Using the Pythagorean theorem:
(3_x_)2 + (4_x_)2 = 102
9_x_2 + 16_x_2 = 100
25_x_2 = 100
_x_2 = 4
x = 2
With x = 2, each side of the square is 4_x_, or 8. The area of a square is length times width. In this case, that's 8 * 8, which is 64.
What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
100
100√2
50√2
50
200√2
Explanation
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
30m
45m
35m
40m
25m
Explanation
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m

Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate 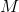
Explanation
The altitude perpendicular to the hypotenuse of a right triangle divides that triangle into two smaller triangles similar to each other and the large triangle. Therefore, the sides are in proportion. The hypotenuse of the triangle is equal to
Therefore, we can set up, and solve for 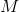

In the figure above, 



Explanation
Assigning the length of ED the value of x, the value of AE will be 3_x_. That makes the entire side AD equal to 4_x_. Since the figure is a square, all four sides will be equal to 4_x_. Also, since the figure is a square, then angle A of triangle ABE is a right angle. That gives triangle ABE sides of 3_x_, 4_x_ and 10. Using the Pythagorean theorem:
(3_x_)2 + (4_x_)2 = 102
9_x_2 + 16_x_2 = 100
25_x_2 = 100
_x_2 = 4
x = 2
With x = 2, each side of the square is 4_x_, or 8. The area of a square is length times width. In this case, that's 8 * 8, which is 64.
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
2√5
11
10√2
15
6√2
Explanation
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Explanation
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
What is the hypotenuse of a right triangle with side lengths 

Explanation
The Pythagorean Theorem states that . This question gives us the values of



Take 



Now we can start solving for 
The length of the hypotenuse is 
What is the hypotenuse of a right triangle with side lengths 

Explanation
The Pythagorean Theorem states that . This question gives us the values of



Take 



Now we can start solving for 
The length of the hypotenuse is 
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
30m
45m
35m
40m
25m
Explanation
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m