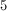All PSAT Math Resources
Example Questions
Example Question #11 : How To Find Median
Find the median
To find the median, arrange the numbers from lowest to highest then find the middle number.
There are two numbers in the middle in this set (

In this case, the median is 6 but you would typically find the average of the two numbers in the middle.
Example Question #12 : How To Find Median
x is the median of this set of numbers: x, 7, 12, 15, 19, 20, 8. What is one possible value of x?
16
18
11
17
14
14
The median is the "middle number" in a sorted list of number; therefore, reorder the numbers in numerical order: 7, 8, 12, 15, 19, 20. Since x is the middle number, it must come between 12 and 15, leaving 14 as the only viable choice.
Example Question #11 : How To Find Median
Craig has a jar full of loose change. He has 20 quarters, 15 dimes, 35 nickels and 55 pennies. If he orders them all from least to most valuable, what is the value of the median coin?
The median is the coin which has an equal number of coins of lesser or equal value and greater or equal value on either side of it. The median therefore falls to one of the nickels (62 quarters, dimes and nickels above it and 62 nickels and pennies below it). The value of a nickel is 5 cents.
Example Question #12 : Median
A student decides to review all of his old tests from his math class in order to prepare for the upcoming exam. The student decides that any exam in which he received a 94% or better he should be able to skip since he understood the material well, but he will review the rest. The first 7 tests are scored out of 50 points. The rest are scored out of 40 points. In order, they got the following raw scores:
The student has 1 more test to add to this list. If he puts together all the tests he must review in order of percentile score, this final test is the median score. Which of the following cannot be the raw score of this final test?
We first remove any 94%+ scores. For tests scored out of 50, a 94% is a 47. Thus anything 47 or greater will be removed. We see that this leaves us with:
For the second half, we have tests scored out of 40. 94% of 40 gives us 37.6, thus we will only remove tests that were a 38 or better. This leaves us with:
Now we have to convert them to percentiles. We end up with the lists as follows. The raw scores are in parentheses:
We then order it by percentile (removing raw scores, as they are unnecessary):
We notice that the median must be between the 78 and the 87.5 percentile scores. 31 out of 40 gives us 77.5%, which is below the score associated with an earlier test. Thus this cannot be the answer. The remaining 4 scores are all higher than 78%, and the largest of them is equal to 87.5 (the highest bound).
Example Question #13 : How To Find Median
In the above set, which of the following is equal to the mean minus the median?
The median is the middle value in an ordered set of numbers. In this instance, we have 8 numbers, so the median is the average of the 4th and 5th number:
The median for this set is 3.5. Now let's find the mean, or the average, of the set:
Now that we have the mean and median, we can finish the question. The question asks for the mean (3.375) minus the median (3.5):
Example Question #1 : How To Find Mode

Looking at the table, what is the difference of the mean minus the mode.
1.0
–1.0
–0.5
0.5
–0.5
The mode is 3 and subtracting 3 from 2.5 gives -0.5.
Example Question #1 : Mode
Find the mode of the following set of numbers:
1, 6, 3, 6, 5, 9
5
6
9
8
6
Mode is the most frequently occuring number in a set. 6 appears most frequently since there are 2 sixes but the rest of the numbers only appear once. The mode is 6
Example Question #1 : How To Find Mode
Find the mode in this set of numbers:
2, 100, 52, 97, 1, 7, 22, 19, 100
100
none of these
2
97
1
100
The mode is the number that appears the most
Example Question #1 : How To Find Mode
Find the mode from the following set of numbers
1, 4, 8, 17, 8, 8, 15, 21, 32, 17
4
15
21
8
17
8
The mode is the number that appears the most in a given set of numbers
Example Question #3 : Mode
Find the mode.
The mode is the number that appears the most often. 9 appears three times.
All PSAT Math Resources