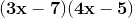All Precalculus Resources
Example Questions
Example Question #1 : Solve A Polynomial By Factoring
Solve the following polynomial for 
The polynomial in the problem is given as follows:
Factoring this polynomial, we would get an expression of the form:
So we need to determine what a and b are. We know we need two factors that when multiplied equal -12, and when added equal -1. If we consider 2 and 6, we could get -12 but could not arrange them in any way that would make their sum equal to -1. We then look at 3 and 4, whose product can be -12 is one of them is negative, and whose sum can be -1 if -4 is added to 3. This tells us that the 4 must be the negative factor and the 3 must be the positive factor, so we get the following:
Example Question #4 : Solving Polynomial Equations
Solve the following polynomial for 
Factoring our polynomial, we can see we will have 2x and x at the beginning of each factor, while we need to find two numbers whose product is 15 and whose sum when multiplied by our leading terms and added is -11x. This gives us the following factorization:
So now we can set each term equal to 0 and solve for our two values of x:
Example Question #1 : Solve A Polynomial By Factoring
Find the root(s) for the function:
The function 

Determine the values of 

Substitute this into the formula.
Set 
Example Question #9 : Solving Polynomial Equations
Solve the following equation:
To solve, factor and then solve for x.
In order to factor we need all our variables and constants on one side. Add 18 to both sides to make our function in a form for which we can factor.
Now we want to find factors of 18 that when added together give us 9. Thus we get the following factored form.
Now set each factor equal to zero and solve for x.
Example Question #5 : Solving Polynomial Equations
Find the zeros of the function 
To find the zeros of the function, you need to factor the equation. Using trial and error, you should arrive at: 


Example Question #51 : Graphing Functions
Solve this polynomial by factoring if it is factorable:
Not factorable
To factor this polynomial it is prudent to recognize that there will only be two factors since the highest power is 
Then ask what numbers multiply to equal postive 35.
Next, what numbers can multiply to equal positive 12.
Let's try 7 and 5 for the last term and 3 and 4 for the first term.
Be sure to put an "x" in the first term of each factor.
Choose the signs based on what the polynomial calls for. In our case we choose negative signs to get positive 35.
Foil these two factors and we get 
All Precalculus Resources