Find the Phase Shift of a Sine or Cosine Function
Help Questions
Pre-Calculus › Find the Phase Shift of a Sine or Cosine Function
Which equation would produce this sine graph?
Explanation
The graph has an amplitude of 2 but has been shifted down 1:
In terms of the equation, this puts a 2 in front of sin, and -1 at the end.
This makes it easier to see that the graph starts \[is at 0\] where 
The phase shift is 

Write the equation for a sine graph with a maximum at 

Explanation
To write this equation, it is helpful to sketch a graph:
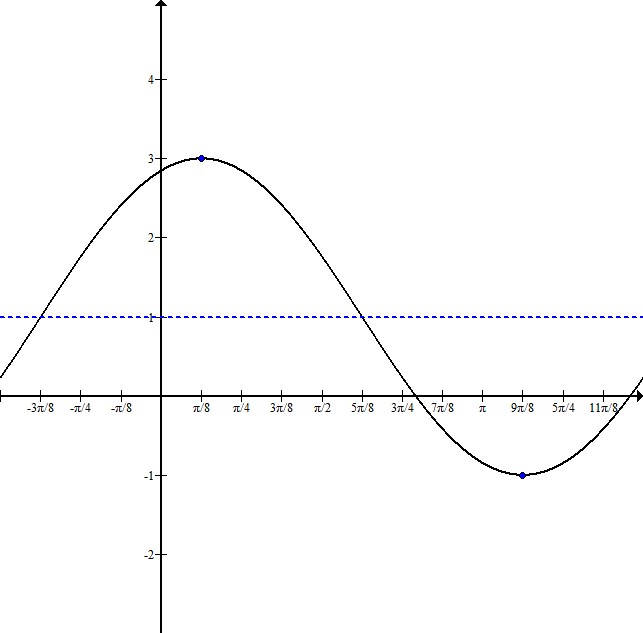
Indicating the maximum and minimum points, we can see that this graph has been shifted up 1, and it has an amplitude of 2.
The distance from the maximum to the minimum point is half the wavelength. In this case, the wavelength is 

This sketch shows that the graph starts to the left of the y-axis. To figure out exactly where, subtract 


Our equation will be in the form 
This graph has an equation of

Write the equation for a cosine graph with a maximum at 

Explanation
In order to write this equation, it is helpful to sketch a graph:
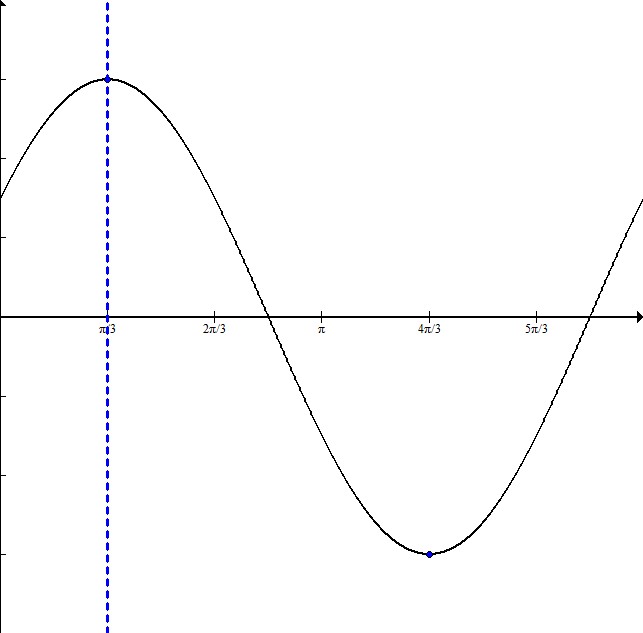
The dotted line is at 

The distance from the maximum to the minimum is half the entire wavelength. Here it is 
Since half the wavelength is 

The amplitude is 3 because the graph goes symmetrically from -3 to 3.
The equation will be in the form 
This equation is

Which equation would produce this graph?
Explanation
This is the graph of sine, but shifted to the right 

Thus resulting in

Write the equation for a sine function with a maximum at 

Explanation
The equation will be in the form 
To write the equation, it is helpful to sketch a graph:
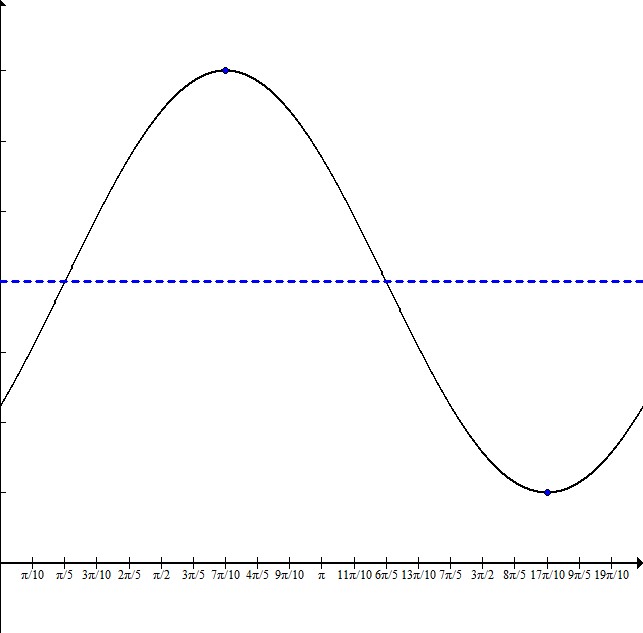
From plotting the maximum and minimum, we can see that the graph is centered on 
The distance from the maximum to the minimum is half the wavelength. For this graph, this distance is 
This means that the total wavelength is 
The graph starts 

Our equation is:

Please choose the best answer from the following choices.
Describe the phase shift of the following function:
Shift left by 
Vertical stretch by 
Shift up by 
Shift down by 
Explanation
Since 

Find the phase shift of 
Explanation
In the formula,


Plugging in what we know gives us:

Simplified, the phase is then 

































