All Pre-Algebra Resources
Example Questions
Example Question #1 : Real Numbers
Which number is the reciprocal of the reciprocal of 
The reciprocal of the reciprocal of any number is the original number. Therefore, the correct choice is 
Example Question #1 : Real Numbers
Order the following numbers from least to greatest.
The main obstacle to solving this problem is the fact that two of the numbers are expressed as fractions while the other two are written as decimals. That means that before we can order them, it might be easiest to change the numbers to either all fractions or all decimals. Changing the fractions to decimals will prove the easier route. You can do this using a calculator by simply dividing the numerator by the denominator. If you do not have a calculator or cannot use one, long division will accomplish the same end. Dividing 3 by 4 in the first fraction results in the decimal 

In math we denote a repeating decimal like this one by putting a bar over the portion that repeats. In other words,
That means that one of the other decimals from our original list is also repeating. Notice that in 
Knowing this we are now able to look at each of the numbers as a decimal. In the number 
Therefore, all of the numbers have a 7 in the tenths place (the first place after the decimal), but 


Therefore, even though 

Since 
Example Question #1 : Real Numbers
Which of the following are real numbers
c and d
a and c
All of the above
b and c
a and b
a and c
a) 

b) 
c) 


d) 
Hence the answer is a and c.
Example Question #1 : Real Numbers
If 
3
-122
122
125
-3
3
The definition of the set of real numbers is the set of all numbers that can fit into a/b where a and b are both integers and b does not equal 0.
So, since we see a fraction here, we know a non-real number occurs if the denominator is 0. Therefore we can find where the denominator is 0 by setting x-3 =0 and solving for x. In this case, x=3 would create a non-real number. Thus our answer is that x CANNOT be 3 for our expression to be a real number.
Example Question #1 : Real Numbers
If 



Therefore, the solution cannot be negative.
Example Question #1961 : Problem Solving Questions
If 

For the expression to be defined, the denominator needs to be different from 0. Therefore:
So the correct answer is 2.
Example Question #3 : Real Numbers
If 

In order to be a real number, 

Therefore, the correct answer is 
Example Question #2 : Real Numbers
Which answer provides a set of real numbers?
All of the above
All of the above
All rational and irrational numbers are considered real numbers, therefore the correct answer is:
All of the above
Example Question #3 : Real Numbers
Which of the following is a real number?
All of them.
All of them.
A real number is considered the union of the sets of rational numbers and irrational numbers. A real number can be positive, negative, fractions, whole numbers, decimals, irrational numbers, etc. Therefore, all of the numbers mentioned are real numbers.
All Pre-Algebra Resources











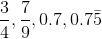




















![x^3 = 8 \Leftrightarrow x = \sqrt[3]{8} \Leftrightarrow x = (2^{3})^{\frac{1}{3}} = 2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/266197/gif.latex)





















