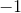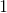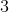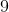Negative Numbers
Help Questions
Pre-Algebra › Negative Numbers

Explanation
This is a straightforward problem. Remember that when adding a negative number, you are actually subtracting:
Be sure to remember that the first number is also negative, meaning we are subtracting a number from a negative number:
The answer is -6.25.
Solve:
Explanation
When solving this problem remember our orders of operation, or PEMDAS.
PEMDAS stands for parentheses, exponents, multiplication/division, and addition/subtraction. When you have a problem with several different operations, you need to solve the problem in this order and you work from left to right for multiplication/division and addition/subtraction.
Evaluate the quantities inside the parentheses first.
Explanation
When two negative values are multiplied, the answer becomes positive. Then, we multiply normally. We should get 

Explanation




Explanation



Answer is
Solve:
Explanation
When dealing with negative numbers, let's see which number is greater. 


Solve:
Explanation
First, since we are multiplying a negative value with a positive value, we need to realize the product is going to be negative. Next, we can multiply the values.
Since the answer is negative, the answer is 
Explanation
When we add a negative number, the sign turns negative. Since we are adding two negative numbers, we treat this as an addition problem and add a minus sign in the end. 
Explanation
To determine the answer, it's best to compare the values without doing any math. Since 





Explanation
When minus signs meet, the sign becomes positive. This becomes an addition problem. Answer is