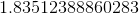All Numerical Methods Resources
Example Questions
Example Question #1 : Numerical Methods
Use Newton's method to determine 


In order to solve this problem, we need to recall newton's method.
So we need to run this equation 4 times
First let's find the derivative of
Now Newton's Method looks like.
Now plug in 4 for
Now we take this answer, and plug it back into the equation for
We keep doing this until, we get to
Below is the results of Newton's Method.
So our final answer will be
Example Question #1 : Numerical Methods
Use Newton's method to determine 


In order to solve this problem, we need to recall newton's method.
So we need to run this equation 4 times
First let's find the derivative of
Now Newton's Method looks like.
Now plug in 4 for
Now we take this answer, and plug it back into the equation for
We keep doing this until, we get to
Below is the results of Newton's Method.
So our final answer will be
Example Question #1 : Numerical Methods
Use Newton's method to determine 


In order to solve this problem, we need to recall newton's method.
So we need to run this equation 3 times
First let's find the derivative of
Now Newton's Method looks like.
Now plug in 3 for
Now we take this answer, and plug it back into the equation for
We keep doing this until, we get to
Below is the results of Newton's Method.
So our final answer will be
Example Question #1 : Numerical Methods
Use Newton's method to determine 


In order to solve this problem, we need to recall newton's method.
So we need to run this equation 4 times
First let's find the derivative of
Now Newton's Method looks like.
Now plug in 4 for
Now we take this answer, and plug it back into the equation for
We keep doing this until, we get to
Below is the results of Newton's Method.
So our final answer will be
Example Question #2 : Numerical Methods
Use Newton's method to determine 


In order to solve this problem, we need to recall newton's method.
So we need to run this equation 2 times
First let's find the derivative of
Now Newton's Method looks like.
Now plug in 2 for
Now we take this answer, and plug it back into the equation for
We keep doing this until, we get to
Below is the results of Newton's Method.
So our final answer will be
Example Question #1 : Algorithms
Use Newton's method to determine 


In order to solve this problem, we need to recall newton's method.
So we need to run this equation 3 times
First let's find the derivative of
Now Newton's Method looks like.
Now plug in 3 for
Now we take this answer, and plug it back into the equation for
We keep doing this until, we get to
Below is the results of Newton's Method.
So our final answer will be
Example Question #3 : Numerical Methods
Use Newton's method to determine 


In order to solve this problem, we need to recall newton's method.
So we need to run this equation 2 times
First let's find the derivative of
Now Newton's Method looks like.
Now plug in 2 for
Now we take this answer, and plug it back into the equation for
We keep doing this until, we get to
Below is the results of Newton's Method.
So our final answer will be
Example Question #1 : Numerical Methods
Use Newton's method to determine 


In order to solve this problem, we need to recall newton's method.
So we need to run this equation 2 times
First let's find the derivative of
Now Newton's Method looks like.
Now plug in 2 for
Now we take this answer, and plug it back into the equation for
We keep doing this until, we get to
Below is the results of Newton's Method.
So our final answer will be
Example Question #9 : Numerical Methods
Use Newton's method to determine 


In order to solve this problem, we need to recall newton's method.
So we need to run this equation 2 times
First let's find the derivative of
Now Newton's Method looks like.
Now plug in 2 for
Now we take this answer, and plug it back into the equation for
We keep doing this until, we get to
Below is the results of Newton's Method.
So our final answer will be
Example Question #3 : Numerical Methods
Use Newton's method to determine 


In order to solve this problem, we need to recall newton's method.
So we need to run this equation 4 times
First let's find the derivative of
Now Newton's Method looks like.
Now plug in 4 for
Now we take this answer, and plug it back into the equation for
We keep doing this until, we get to
Below is the results of Newton's Method.
So our final answer will be
All Numerical Methods Resources