All MCAT Physical Resources
Example Questions
Example Question #1 : Equilibrium
Which of the following statements is false about the Keq of a reversible chemical reaction?
Pure liquid and solid concentrations are found in the Keq equation
Keq is not affected by catalysts
Keq is tempurature dependent
As Keq increases, the equilibrium concentration of products in the reaction increases
Pure liquid and solid concentrations are found in the Keq equation
Keq only includes the concentrations of gases and aqueous solutions. Pure solid and liquid concentrations are left out of the equation.
Keq is given by the equation below, where the concentrations expressed are the equilibrium concentrations.
Keq is a property of a given reaction at a given temperature. It is unaffected by catalysts, which only affect rate and activation energy. As the value of Keq increases, the equilibrium concentration of products must also increase, based on the equation.
Example Question #1 : Equilibrium
For any given chemical reaction, one can draw an energy diagram. Energy diagrams depict the energy levels of the different steps in a reaction, while also indicating the net change in energy and giving clues to relative reaction rate.
Below, a reaction diagram is shown for a reaction that a scientist is studying in a lab. A student began the reaction the evening before, but the scientist is unsure as to the type of the reaction. He cannot find the student’s notes, except for the reaction diagram below.

Eventually, the reaction reaches equilibrium. The scientist makes a change to the reaction vessel, and again measures Q. He now finds that Q is greater than the value of the Keq he had measured when the reaction was at equilibrium. Since Q > Keq, what value is equal to the first activation energy that must be overcome as the reaction returns to equilibrium?
The energy difference between points 4 and 5
The energy difference between points 3 and 4
The energy difference between points 3 and 5
The energy difference between points 2 and 3
The energy difference between points 1 and 2
The energy difference between points 4 and 5
Because Q is now greater than Keq, we know that we need to run the reaction in reverse to come back to equilibrium, where Q = Keq. A larger Q value indicates that [products] must be decreased in order to equilibrate at Keq.
The first activation energy we have to overcome in the conversion of products to reactants is the difference between the energy of the products (point 5) and the first transition state (point 4) relative to the products.
Example Question #3 : Equilibrium Constant And Reaction Quotient
Write the law of mass action for the given reaction.
The law of mass action is used to compare the chemical equation to the equilibrium constant. In the equation, the product concentration are on the top, and the reactant concentrations are on the bottom. Coefficients in the balanced equation become the exponents seen in the equilibrium equation. While pure solids and liquids can be excluded from the equation, pure gases must still be included.
Example Question #2 : Equilibrium
The partial pressures of H2 and CH3OH are 0.5atm and 1.4atm respectively. What is the partial pressure of CO if the reaction is at equilibrium?
More information is needed in order to answer the question.
If the reaction is at equilibrium, we know that the law of mass action will equal the equilibrium constant given in the above information. When the reaction contains only gases, partial pressure values can be substituted for concentrations. As a result, we simply need to add the values into the equation and solve for the partial pressure of carbon monoxide (CO).
Example Question #761 : Mcat Physical Sciences
A scientist is studying a reaction, and places the reactants in a beaker at room temperature. The reaction progresses, and she analyzes the products via NMR. Based on the NMR readout, she determines the reaction proceeds as follows:
In an attempt to better understand the reaction process, she varies the concentrations of the reactants and studies how the rate of the reaction changes. The table below shows the reaction concentrations as she makes modifications in three experimental trials.
Which of the following are true when the reaction reaches equilibrium?
I. The energy levels of the reactants and products will be equal
II. The reaction rate of the forward and reverse reactions will be equal
III. The concentrations of the reactants and products will be equal
III only
I, II, and III
I and II
II and III
II only
II only
When a reaction reaches equilibrium, the forward and reverse reaction rates are equal. The arrival of a reaction at equilibrium does not speak to the concentrations. Arrival at equilibrium also does not change the inherent energy properties of the reactants and products.
Example Question #762 : Mcat Physical Sciences
A scientist is studying a reaction, and places the reactants in a beaker at room temperature. The reaction progresses, and she analyzes the products via NMR. Based on the NMR readout, she determines the reaction proceeds as follows:
In an attempt to better understand the reaction process, she varies the concentrations of the reactants and studies how the rate of the reaction changes. The table below shows the reaction concentrations as she makes modifications in three experimental trials.
At a particular time point the reaction quotient of the above reaction is calculated to be 1.5. The equilibrium constant at the specific conditions assumed in the passage is 0.06. Which of the following statements is true regarding the reaction equilibrium?
As the reaction comes to equilibrium, the concentration of the reactants will decrease
As the reaction comes to equilibrium, the concentration of the reactants will first decrease, and then increase
As the reaction comes to equilibrium, the concentration of the reactants will first increase, and then decrease
As the reaction comes to equilibrium, the concentration of the reactants will remain unchanged
As the reaction comes to equilibrium, the concentration of the reactants will increase
As the reaction comes to equilibrium, the concentration of the reactants will increase
If the reaction quotient is larger than the equilibrium constant, then there is a relative abundance of products compared to their equilibrium concentration. By proxy, there must be a deficiency of reactants with respect to the equilibrium concentrations. The reactants will need to increase in concentration until the reaction reaches equilibrium.
Example Question #3 : Equilibrium
The initial concentrations of this reaction are listed below.
Based on these initial concentrations, which statement is true?
The reaction will shift left
The forward rate will be greater than the reverse rate
The ratio of products to reactants is greater than the equilibrium constant
The reaction is in equilibrium
The forward rate will be greater than the reverse rate
When given initial concentrations, we can determine the reaction quotient (Q) of the reaction. The reaction quotient is given by the same equation as the equilibrium constant (concentration of products divided by concentration of reactants), but its value will fluctuate as the system reacts, whereas the equilibrium constant is based on equilibrium concentrations.
By comparing the reaction quotient to the equilibrium constant, we can determine in which direction the reaction will proceed initially.
The reaction quotient with the beginning concentrations is written below.
This shows that the ratio of products to reactants is less than the equilibrium constant. Since Q is less than Keq in the beginning, we conclude that the reaction will proceed forward until Q is equal to Keq. In this manner, the denominator (reactants) will decrease and the numerator (products) will increase, causing Q to become closer to Keq.
Example Question #8 : Equilibrium Constant And Reaction Quotient
A scientist prepares an experiment to demonstrate the second law of thermodynamics for a chemistry class. In order to conduct the experiment, the scientist brings the class outside in January and gathers a cup of water and a portable stove.
The temperature outside is –10 degrees Celsius. The scientist asks the students to consider the following when answering his questions:
Gibbs Free Energy Formula:
ΔG = ΔH – TΔS
Liquid-Solid Water Phase Change Reaction:
H2O(l) ⇌ H2O(s) + X
The scientist prepares two scenarios.
Scenario 1:
The scientist buries the cup of water outside in the snow, returns to the classroom with his class for one hour, and the class then checks on the cup. They find that the water has frozen in the cup.
Scenario 2:
The scientist then places the frozen cup of water on the stove and starts the gas. The class finds that the water melts quickly.
After the water melts, the scientist asks the students to consider two hypothetical scenarios as a thought experiment.
Scenario 3:
Once the liquid water at the end of scenario 2 melts completely, the scientist turns off the gas and monitors what happens to the water. Despite being in the cold air, the water never freezes.
Scenario 4:
The scientist takes the frozen water from the end of scenario 1, puts it on the active stove, and the water remains frozen.
The same scientist in the passage measures the variables of another reaction in the lab. He knows that this reaction is spontaneous under standard conditions, with a standard free energy change of –43 kJ/mol. Using laboratory-calculated variables, he determines that the Gibbs Free Energy has a value of 0 kJ/mol. He then calculated the reaction quotient of this reaction, while knowing the equilibrium constant was 3 x 103. What is true of the reaction quotient?
It must be one
It must be less than 3 x 103
It must be more than 3 x 103
It must be equal to 3 x 103
It must be zero
It must be equal to 3 x 103
At equilibrium, reaction quotient and equilibrium constant are equal.
Example Question #1 : Equilibrium
For any given chemical reaction, one can draw an energy diagram. Energy diagrams depict the energy levels of the different steps in a reaction, while also indicating the net change in energy and giving clues to relative reaction rate.
Below, a reaction diagram is shown for a reaction that a scientist is studying in a lab. A student began the reaction the evening before, but the scientist is unsure as to the type of the reaction. He cannot find the student’s notes, except for the reaction diagram below.

The scientist in the passage is able to calculate the reaction quotient (Q) for the reaction taking place in the vessel. If the reaction is ongoing, and has not yet reached equilibrium, how will the reaction quotient compare to the reaction constant (Keq)?
(Assume the reaction is in aqueous solution and is started with 100% reactants and no products).
Keq and Q will be equal
Q will be less than Keq
Q will be zero, and Keq will be greater than 1
Keq will be zero, and Q will be greater than 1
Keq will be less than Q
Q will be less than Keq
At equilibrium, Keq = Q. The question indicates that, starting with 100% reactants, the reaction has not yet reached equilibrium. In order to reach equilibrium, we must have a continued reduction in reactants and accumulation of products. This would necessitate an increase in Q to eventually reach the value of Keq. Essentially, Q is starting at zero and increasing to the value of Keq at equilibrium.
Example Question #15 : Analytical Chemistry
In the above reaction, by what factor would the reaction quotient change if the concentration of 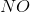
No change
For a general chemical equation 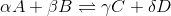
We can find the reaction quotient equation for our reaction by substituting the variables.
Notice that the concentration of 

All MCAT Physical Resources

![K_{eq}=\frac{[products]}{[reactants]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/85202/gif.latex)
![Q=\frac{[products]}{[reactants]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/132165/gif.latex)
![K_{eq}=\frac{[equilibrium\ product]}{[equilibrium\ reactant]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/85250/gif.latex)


![K_{eq} = \frac{[CH_{3}OH]}{[CO]2[H_{2}]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/30160/gif.latex)
![K_{eq} = \frac{[CH_{3}OH]}{[CO][H_{2}]^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/30159/gif.latex)
![K_{eq}=\frac{[CH_3OH]}{[CO]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/30161/gif.latex)
![K_{eq} = \frac{[CO][H_{2}]^{2}}{[CH_{3}OH]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/30162/gif.latex)
![aA+bB\rightarrow cC\ K_{eq}=\frac{[C]^c}{[A]^a[B]b}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/85996/gif.latex)
![CO(g) + 2H_{2}(g) \rightarrow CH_{3}OH(g)\ K_{eq}=\frac{[CH_3OH]}{[CO][H_2]^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/110360/gif.latex)









![\begin{matrix} Trial & [NH_4^+] & [NO_2^-] &Rate \\ 1& 0.480M &0.120M &0.018\frac{M}{s} \\ 2& 0.240M & 0.120M& 0.009\frac{M}{s}\\ 3& 0.240M& 0.360M & 0.027\frac{M}{s} \end{matrix}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/117028/gif.latex)

![\begin{matrix} Trial & [NH_4^+] & [NO_2^-] &Rate \\ 1& 0.480M &0.120M &0.018\frac{M}{s} \\ 2& 0.240M & 0.120M& 0.009\frac{M}{s}\\ 3& 0.240M& 0.360M & 0.027\frac{M}{s} \end{matrix}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/95871/gif.latex)


![[CH_{3}OH] = 2.5M, [CO] = 1.3M, [H_{2}] =0.6M.](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/115362/gif.latex)
![Q=\frac{[CO][H_2]^2}{[CH_3OH]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/183371/gif.latex)
![Q\ \text{or}\ K_{eq}=\frac{[CH_3OH]}{[H_2]^2[CO]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/183372/gif.latex)
![\frac{[2.5]}{[0.6]^{2}[1.3]} = 5.3](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/86003/gif.latex)
![Q=\frac{[products]}{[reactants]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/110330/gif.latex)
![K_{eq}=\frac{[equilibrium\ product]}{[equilibrium\ reactant]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/85249/gif.latex)
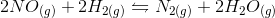




![Q=\frac{[C]^{\gamma}[D]^{\delta}}{[A]^{\alpha}[B]^{\beta}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/668140/gif.latex)

![Q=\frac{[N_{2}][H_{2}O]^{2}}{[NO]^{2}{[H_{2}]}^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/668141/gif.latex)
![Q_2=\frac{[N_{2}][H_{2}O]^{2}}{[2NO]^{2}{[H_{2}]}^{2}}=\frac{[N_{2}][H_{2}O]^{2}}{4[NO]^{2}{[H_{2}]}^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/668142/gif.latex)




