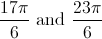All High School Math Resources
Example Questions
Example Question #3 : Angles
Which of the following angles is coterminal with 
For an angle to be coterminal with 









Example Question #1 : Understanding Coterminal Angles
Find a coterminal angle for 
Coterminal angles are angles that, when drawn in the standard position, share a terminal side. You can find these angles by adding or subtracting 360 to the given angle. Thus, the only angle measurement that works from the answers given is 
Example Question #22 : Trigonometry
Which of the following angles is coterminal with 
Each angle given in the other choices is coterminal with 
Each angle given in the other choices is coterminal with 
For an angle to be coterminal with 







All four choices pass the test, so all four angles are coterminal with 
Example Question #1 : Understanding Coterminal Angles

Example Question #2 : Understanding Coterminal Angles
Which of the following choices represents a pair of coterminal angles?
For two angles to be coterminal, they must differ by 







The only angles that pass the test - and are therefore coterminal - are 
Certified Tutor
Certified Tutor
All High School Math Resources










![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{2\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99513/gif.latex)


![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{9\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99515/gif.latex)


![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{12\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99517/gif.latex)