Angles
Help Questions
Math › Angles
What angle is complementary to 
Explanation
Two complementary angles add up to 
Therefore, 
What angle is complementary to 
Explanation
Two complementary angles add up to 
Therefore, 
Which of the following choices represents a pair of coterminal angles?
Explanation
For two angles to be coterminal, they must differ by 







The only angles that pass the test - and are therefore coterminal - are 
Which of the following choices represents a pair of coterminal angles?
Explanation
For two angles to be coterminal, they must differ by 







The only angles that pass the test - and are therefore coterminal - are 
What angle is supplementary to 
Explanation
Supplementary angles add up to 
Which of the following angles is coterminal with 
Explanation
For an angle to be coterminal with 









What angle is supplementary to 
Explanation
Supplementary angles add up to 
Which of the following angles is coterminal with 
Explanation
For an angle to be coterminal with 



















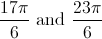























![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{2\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99513/gif.latex)


![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{9\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99515/gif.latex)


![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{12\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99517/gif.latex)


 and
and  .
.



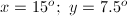
 all reside along one line, therefore, their sum must be
all reside along one line, therefore, their sum must be 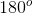 .
.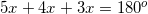


 and
and 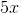 are opposite angles, they must be equal.
are opposite angles, they must be equal.


