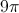All High School Math Resources
Example Questions
Example Question #21 : Cylinders
What is the volume of a cylinder with a radius of 

When thinking of a 3D figure, think of it as a stack of something. In this case, a cylinder is a stack of a circles.
The volume will be the area of that base circle times the height of the cylinder. Mathematically that would be 
Plug in our given values and solve.
Example Question #22 : Cylinders
Find the volume of a cylinder given that its height and radius are 4 and 11, respectively.
The standard equation to find the volume of a cylinder is
where 

Plug in the given values for height and radius to find the volume of the cylinder:
Example Question #23 : Cylinders
Find the volume of the following cylinder.

The formula for the volume of a cylinder is:
where 

Plugging in our values, we get:
Example Question #24 : Cylinders
Find the volume of the following cylinder.

The formula for the volume of a cylinder is:
Where 

Plugging in our values, we get:
Example Question #111 : Solid Geometry
Find the volume of the following partial cylinder.

The formula for the volume of a partial cylinder is:
Where 


Plugging in our values, we get:
Example Question #1971 : High School Math
Find the volume of the following partial cylinder.

The formula for the volume of a partial cylinder is:
where 


Plugging in our values, we get:
Example Question #1 : How To Find The Surface Area Of A Cylinder
If a cylinder has a radius, 

The total surface area will be equal to the area of the two bases added to the area of the outer surface of the cylinder. If "unwrapped" the area of the outer surface is simply a rectangle with the height of the cylinder and a base equal to the circumference of the cylinder base. We can use these relationships to find a formula for the total area of the cylinder.
Use the given radius and height to solve for the final area.
Example Question #2 : How To Find The Surface Area Of A Cylinder
The volume of a cylinder is 

The volume of a cylinder is equal to:
Use this formula and the given radius to solve for the height.
Now that we know the height, we can solve for the surface area. The surface area of a cylinder is equal to the area of the two bases plus the area of the outer surface. The outer surface can be "unwrapped" to form a rectangle with a height equal to the cylinder height and a base equal to the circumference of the cylinder base. Add the areas of the two bases and this rectangle to find the total area.
Use the radius and height to solve.
Example Question #21 : Cylinders
What is the surface area of a cylinder with a base diameter of 

None of the answers
Area of a circle
Circumference of a circle
Surface area of a cylinder
Example Question #30 : Cylinders
A balloon, in the shape of a sphere, is filled completely with water. The surface area of the filled balloon is 
The surface area of a sphere is given by the formula


To find out what the water level would be, we need to know how much water is in the balloon. So we need to find the volume of the balloon.
The amount of water that is in the balloon is
=
The cylindrical column of water will have this volume, and will have base radius 4. Using the formula for volume of a cylinder, we can solve for the height of the column of water.


All High School Math Resources