Introduction to Functions
Help Questions
Math › Introduction to Functions
Which of the following is NOT a function?
Explanation
A function has to pass the vertical line test, which means that a vertical line can only cross the function one time. To put it another way, for any given value of 












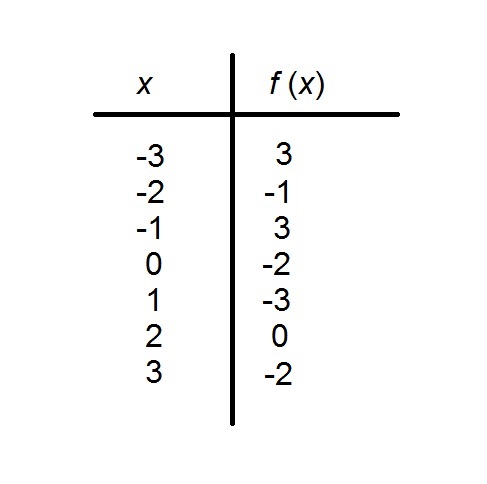
The above table shows a function with domain 
True or false: 
False
True
Explanation
A function 




If we order the rows by range value, we see this to not be the case:



If 


Explanation
Evaluate 


Distribute the integer through the binomial and simplify the equation.
Multiply this expression with 
The answer is:
If 

Explanation
Substitute the assigned values into the expression.
Simplify the inside parentheses.
The answer is:
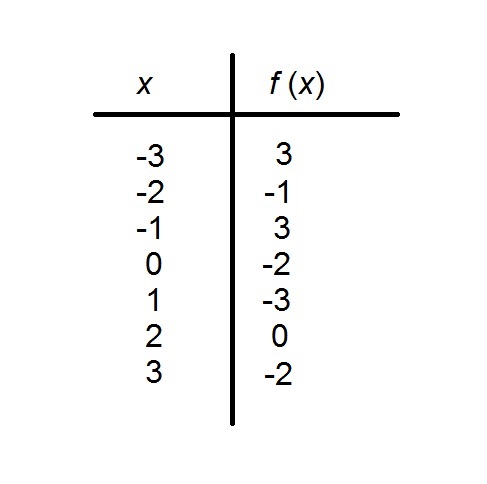
The above table shows a function with domain 
True or false: 
False
True
Explanation
A function 




If we order the rows by range value, we see this to not be the case:



Determine the inverse:
Explanation
In order to find the inverse of this function, interchange the x and y-variables.
Subtract three from both sides.
Simplify the equation.
Divide by ten on both sides.
Simplify both sides.
The answer is:
What is the domain of the function 
Explanation
The expression under the square root symbol cannot be negative, so to find the domain, set that expression 
The domain includes all x-values less than or equal to 7, which can be written as ![(-\infty,7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/606895/gif.latex)
Determine the inverse of:
Explanation
Interchange the x and y-variables.
Solve for y. Add one-half on both sides.
Simplify both sides.
Multiply five over two on both sides in order to isolate the y-variable.
Apply the distributive property on the left side. The right side will reduce to just a lone y-variable.
The answer is:
If 


Explanation
Evaluate 


Distribute the integer through the binomial and simplify the equation.
Multiply this expression with 
The answer is:
Find the range of the following equation:
Explanation
Expand the quadratic.
Use the FOIL method to expand the binomials.
The equation becomes:
Now that we have the equation in 
The formula is:
Substitute the values.
To find the y-value, substitute the x-value back to the original equation.
The minimum is:
Because the value of 
The range is:





































![(-\infty, 7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/606876/gif.latex)

![(-\infty, 2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/606863/gif.latex)





















![(-\infty,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/733455/gif.latex)
![(-\infty,0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/733456/gif.latex)








