All GRE Math Resources
Example Questions
Example Question #1 : How To Graph An Inequality With A Number Line
On a real number line, x1 = -4 and x2 = 14. What is the distance between these two points?
4
18
-18
10
18
The distance between two points is always positive. We calculate lx2 - x1l, which will give us the distance between the points.
|14- (-4)| = |14+4| = |18| = 18
Example Question #1 : Number Line
Which of the following is a graph for the values of 



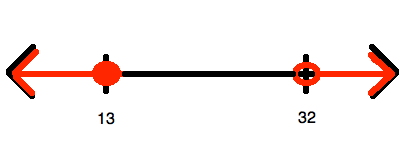


To begin, you must simplify so that you "isolate" 

Now, this inequality represents all of the numbers between 13 and 32. However, it does include 


Example Question #11 : Number Lines And Absolute Value

Which of the following inequalities is represented by the number line shown above?
Since the inequality represents one range of values between two end points (both of which are included, given the sign being "less than or equal"), you know that whatever you answer, it must be convertible to the form:
Now, you know that it is impossible to get this out of the choices that have no absolute values involved in them. Therefore, the only options that make sense are the two having absolute values; however, here you should choose only the ones that have a 
The wrong answer is simplified in this manner:
And you can stop right here, for you know you will never have 
The other option is simplified in this manner:
This is just what you need!
Example Question #2 : Number Line
Quantity A:
Quantity B:
The relationship cannot be determined.
Quantity B is larger.
The two quantities are equal.
Quantity A is larger.
Quantity B is larger.
It is not necessary to solve this problem by multiplying terms out. Notice that between quantities A and B, the last three terms switch places for the two large numbers. as such they can be rewritten:
Quantity A:
Quantity B:
Both quantities A and B share the exact same terms, save for two:
Quantity A:
Quantity B:
From visual inspection, it is clear that B is larger.
Example Question #122 : Arithmetic

Which of the following is true?
Since 


For the A, it is possible to choose values that make the statement false, for example 

C is always false.
Example Question #123 : Arithmetic

Which of the statements is always true?
Although C may approach zero for large values of 

A and B, however, have x and y values which make them false:
For A, an example is
For B, 
Example Question #12 : Number Lines And Absolute Value
Which of the following is a graph for the values of 






Begin by solving for 
Now, this is represented by drawing an open circle at 6 and graphing upward to infinity:

All GRE Math Resources