All GRE Math Resources
Example Questions
Example Question #1 : Apply The Pythagorean Theorem To Find The Distance Between Two Points In A Coordinate System: Ccss.Math.Content.8.G.B.8
Daria and Ashley start at the same spot and walk their two dogs to the park, taking different routes. Daria walks 1 mile north and then 1 mile east. Ashley walks her dog on a path going northeast that leads directly to the park. How much further does Daria walk than Ashley?
2 – √2 miles
2 + √2 miles
1 mile
√2 miles
Cannot be determined
2 – √2 miles
First let's calculate how far Daria walks. This is simply 1 mile north + 1 mile east = 2 miles. Now let's calculate how far Ashley walks. We can think of this problem using a right triangle. The two legs of the triangle are the 1 mile north and 1 mile east, and Ashley's distance is the diagonal. Using the Pythagorean Theorem we calculate the diagonal as √(12 + 12) = √2. So Daria walked 2 miles, and Ashley walked √2 miles. Therefore the difference is simply 2 – √2 miles.
Example Question #961 : High School Math
Which of the following sets of sides cannnot belong to a right triangle?
5, 12, 13
2, 2, 2√2
3, 4 ,5
6, 7, 8
2, 2√3, 4
6, 7, 8
To answer this question without plugging all five answer choices in to the Pythagorean Theorem (which takes too long on the GRE), we can use special triangle formulas. Remember that 45-45-90 triangles have lengths of x, x, x√2. Similarly, 30-60-90 triangles have lengths x, x√3, 2x. We should also recall that 3,4,5 and 5,12,13 are special right triangles. Therefore the set of sides that doesn't fit any of these rules is 6, 7, 8.
Example Question #111 : Geometry
Max starts at Point A and travels 6 miles north to Point B and then 4 miles east to Point C. What is the shortest distance from Point A to Point C?
2√13 miles
4√2 miles
7 miles
10 miles
5 miles
2√13 miles
This can be solved with the Pythagorean Theorem.
62 + 42 = c2
52 = c2
c = √52 = 2√13
Example Question #11 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
Which set of side lengths CANNOT correspond to a right triangle?
3, 4, 5
5, 12, 13
8, 15, 17
7, 24, 25
6, 8, 11
6, 8, 11
Because we are told this is a right triangle, we can use the Pythagorean Theorem, a2 + b2 = c2. You may also remember some of these as special right triangles that are good to memorize, such as 3, 4, 5.
Here, 6, 8, 11 will not be the sides to a right triangle because 62 + 82 = 102.
Example Question #22 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
Kathy and Jill are travelling from their home to the same destination. Kathy travels due east and then after travelling 6 miles turns and travels 8 miles due north. Jill travels directly from her home to the destination. How miles does Jill travel?
Kathy's path traces the outline of a right triangle with legs of 6 and 8. By using the Pythagorean Theorem


Example Question #1 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
Square 






Quantity A:
Quantity B: The distance between points 
Quantity A is greater.
The relationship cannot be determined from the information provided.
The two quantities are equal.
Quantity B is greater.
The two quantities are equal.
To find the distance between points 



Example Question #101 : Plane Geometry
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?


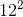

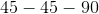
All GRE Math Resources
















