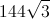All GRE Math Resources
Example Questions
Example Question #2 : Equilateral Triangles
What is the area of an equilateral triangle with a base of 
An equilateral triangle can be considered to be 2 identical 30-60-90 triangles, giving the triangle a height of 
Example Question #3 : Equilateral Triangles

An equilateral triangle is inscribed into a circle of radius 10. What is the area of the triangle?
The answer cannot be determined from the information given.
To solve this equation, first note that a line drawn from the origin to a vertex of the equilateral triangle will bisect the angle of the vertex. Furthermore, the length of this line is equal to the radius:

That this creates in turn is a 30-60-90 right triangle. Recall that the ratio of the sides of a 30-60-90 triangle is given as:
Therefore, the length of the 
This is also one half of the base of the triangle, so the base of the triangle can be found to be:
Furthermore, the length of the 
The vertical section rising from the origin is the length of the radius, which when combined with the shorter section above gives the height of the triangle:
The area of a triangle is given by one half the base times the height, so we can find the answer as follows:
Example Question #4 : Equilateral Triangles
Find the area of an equilateral triangle when one of its sides equals 4.
8
2√3
4
4√3
4√3
All sides of an equilateral triangle are equal, so all sides of this triangle equal 4.
Area = 1/2 base * height, so we need to calculate the height: this is easy for an equilateral triangle, since you can bisect any such triangle into two identical 30:60:90 triangles.
The ratio of lengths of a 30:60:90 triangle is 1:√3:2. The side of the equilateral triangle is 4, and we divided the base in half when we bisected the triangle, so that give us a length of 2, so our triangle must have sides of 2, 4, and 2√3; thus we have our height.
One of our 30:60:90 triangles will have a base of 2 and a height of 2√3. Half the base is 1, so 1 * 2√3 = 2√3.
We have two of these triangles, since we divided the original triangle, so the total area is 2 * 2√3 = 4√3.
You can also solve for the area of any equilateral triangle by applying the formula (s2√3)/4, where s = the length of any side.
All GRE Math Resources