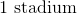All Common Core: 7th Grade Math Resources
Example Questions
Example Question #81 : Ratios & Proportional Relationships
Armen can complete 

The phrase "per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have amount of homework, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
Armen can complete 
Example Question #81 : Ratios & Proportional Relationships
A baker can decorate 

The phrase "per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have the portion of the cake decorated, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
The baker can decorate 
Example Question #83 : Ratios & Proportional Relationships
A painter can paint 

The phrase "per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have portion of the house painted, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
The painter can paint 
Example Question #82 : Ratios & Proportional Relationships
A janitor can clean 

The phrase "per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have the portion of the stadium, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
The janitor can clean 
Example Question #81 : Compute Unit Rates Associated With Ratios Of Fractions: Ccss.Math.Content.7.Rp.A.1
Andrew spends every Saturday at the gym working out. He can complete 

The phrase "per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have the portion of his workout, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
Andrew can complete 
Example Question #84 : Ratios & Proportional Relationships
Andrew spends every Saturday at the gym working out. He can complete 

The phrase "per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have the portion of his workout, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
Andrew can complete 
Example Question #82 : Compute Unit Rates Associated With Ratios Of Fractions: Ccss.Math.Content.7.Rp.A.1
Eric walks one-fourth of a mile in half an hour. If he continues at this rate, what is Eric's speed in miles per hour 
The phrase "miles per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have miles, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
Eric can walk at a speed of:
Example Question #81 : Compute Unit Rates Associated With Ratios Of Fractions: Ccss.Math.Content.7.Rp.A.1
Stuart used 

1
2
1.5
3
0.5
1
The phrase "bags of oranges does he use per gallon" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have bags of oranges, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
Stuart will use 
Certified Tutor
Certified Tutor
All Common Core: 7th Grade Math Resources