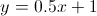To find the equation of the line at that point, you need two things: the slope at that point and the y adjustment of the function, in the form , where m is the slope and is the y adjustment. To get the slope, find the derivative of and plug in the desired point for , giving us an answer of for the slope.

To find the y adjustment pick a point 0 in the original function. For simplicity, let's plug in , which gives us a y of 1, so an easy point is . Next plug in those values into the equation of a line, . The new equation with all parameters plugged in is

Now you simply solve for , which is .

Final equation of the line tangent to at is

First, take the derivative of f(x). This is very easy:

f'(x) = 12x2 – 4x

Now, the slope of the tangent line at x = 5 is f'(5). Evaluated, this is: f'(5) = 12 * 5 * 5 – 4 * 5 = 300 – 20 = 280

Now, we must find the intersection point on the original line:

f(5) = 4 * 53 – 2 * 52 + 4 = 500 – 50 + 4 = 454

Therefore, the point of tangent intersection is (5,454).

Using the point-slope form of linear equations, we can find the line:

(y – 454) = 280(x – 5)

y – 454 = 280x – 1400

y = 280x – 946

To get the slope, find the derivative of and plug in the desired point for , giving us an answer of for the slope.

Remember that the derivative of .

To find the adjustment pick a point (for example) in the original function. For simplicity, let's plug in , which gives us a of , so an easy point is . Next plug in those values into the equation of a line, . The new equation with all parameters plugged in is

The coefficient in front of the is the slope.

Now you simply solve for , which is .

Final equation of the line tangent to at is .

In order to find the slope of the tangent line through a certain point, we must find the rate of change (derivative) of the function. The derivative of is written as . This tells us what the slope of the tangent line is through any point in our function . In other words, all we need to do is plug-in (because our point has an x-value of 1) into . This will give us our answer, .

The tangent line to at must have the same slope as .

Applying the chain rule we get

.

Therefore the slope of the line is,

.

In addition, the tangent line touches the graph of at . Since , the point lies on the line.

Plugging in the slope and point we get .

To find the tangent line one must first find the slope, this can be given by the derivative evaluated at a point.

To find the derivative of this function use the power rule which states,

The derviative of is .

Evaluated at our point ,

we find that the slope, m is also 3.

Now we may use the point-slope equation of a line to find the tangent line.

The point slope equation is

Where is the point at which the line is tangent.

Using this definition we find the tangent line to be defined by .

The equation of the tangent line has the form .

The slope can be determined by evaluating the derivative of the function at .

Plugging this into the point slope equation, we get

can be determined by evaluating the original function at .

Plugging this into the previous equation and simplifying gives us

The equation of the tangent line will have the form , where is the slope of the line and .

To find the slope, we need to evaluate the derivative at :

Now that we have the slope, we can determine the equation of the tangent line using the point-slope formula:

To find the slope of the line tangent you must take the derivative of the function. The derivative of cosine is negative sine and the derivative of sine is cosine.

This makes the derivative of the function

.

Plug in the given x to get the slope.

First, evaluate when .

Thus, we need a line that contains the point

Next, find the derivative of and evaluate it at .

To find the derivative we will use the power rule,

.

This indicates that we need a line with a slope of 8.

In point-slope form, , a line with the point and a slope of 8 will be: