Confidence Intervals and Regression
Help Questions
AP Statistics › Confidence Intervals and Regression
The number of hamburgers served by McGregors per day is normally distributed and has a mean of 


Explanation
First, find the first quartile of the distribution.
Then, find the third quartile of the distribution.
Which of the following statements are correct about confidence intervals?
The width of a confidence interval decreases as the sample size increases and increases as the confidence level increases.
The width of a confidence interval increases as the sample size increases and increases as the confidence level increases.
The width of a confidence interval decreases as the sample size increases and increases as the confidence level decreases.
The width of a confidence interval increases as the sample size increases and increases as the confidence level decreases.
The width of a confidence interval does not change as the sample size increases and increases as the confidence level increases.
Explanation
Larger samples give narrower intervals. We are able to estimate a population proportion more precisely with a larger sample size.
As the confidence level increases the width of the confidence interval also increases. A larger confidence level increases the chance that the correct value will be found in the confidence interval. This means that the interval is larger.
Jim calculated a 

In the long run, 

There is a 

More information is needed.
Explanation
95% confidence means that the methods Jim uses to calculate his confidence interval give him correct results 95% of the time. It does not mean that there is a 95% chance that the true mean will be inside the interval. It also does not mean that 95% of all heights or possible sample means fall within the interval.
Jim calculated a 

In the long run, 

There is a 

More information is needed.
Explanation
95% confidence means that the methods Jim uses to calculate his confidence interval give him correct results 95% of the time. It does not mean that there is a 95% chance that the true mean will be inside the interval. It also does not mean that 95% of all heights or possible sample means fall within the interval.
Which of the following statements are correct about confidence intervals?
The width of a confidence interval decreases as the sample size increases and increases as the confidence level increases.
The width of a confidence interval increases as the sample size increases and increases as the confidence level increases.
The width of a confidence interval decreases as the sample size increases and increases as the confidence level decreases.
The width of a confidence interval increases as the sample size increases and increases as the confidence level decreases.
The width of a confidence interval does not change as the sample size increases and increases as the confidence level increases.
Explanation
Larger samples give narrower intervals. We are able to estimate a population proportion more precisely with a larger sample size.
As the confidence level increases the width of the confidence interval also increases. A larger confidence level increases the chance that the correct value will be found in the confidence interval. This means that the interval is larger.
The number of hamburgers served by McGregors per day is normally distributed and has a mean of 


Explanation
First, find the first quartile of the distribution.
Then, find the third quartile of the distribution.
You are asked to create a 


Explanation
Keep in mind that the margin of error for a confidence interval based on a normal population is equal to 


From the problem, we can tell that 


The minimum sample size is 



You are asked to create a 


Explanation
Keep in mind that the margin of error for a confidence interval based on a normal population is equal to 


From the problem, we can tell that 


The minimum sample size is 



You estimate a regression model with 



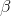
Explanation
To construct 95% confidence intervals for 



You estimate a regression model with 



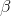
Explanation
To construct 95% confidence intervals for 



















![\left [ 3.35,3.45 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/37119/gif.latex)
![\left [ 3.4,3.45 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/37120/gif.latex)
![\left [ 3.1,3.45 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/37121/gif.latex)