All AP Statistics Resources
Example Questions
Example Question #1 : Confidence Intervals And Mean
Suppose you have a normally distributed variable with known variance. How many standard errors do you need to add and subtract from the sample mean so that you obtain 95% confidence intervals?
To obtain 95% confidence intervals for a normal distribution with known variance, you take the mean and add/subtract 
Example Question #2 : Confidence Intervals And Mean
An automotive engineer wants to estimate the cost of repairing a car that experiences a 25 MPH head-on collision. He crashes 24 cars, and the average repair is $11,000. The standard deviation of the 24-car sample is $2,500.
Provide a 98% confidence interval for the true mean cost of repair.
Standard deviation for the samle mean:
Since n < 30, we must use the t-table (not the z-table).
The 98% t-value for n=24 is 2.5.
Example Question #1 : How To Find Confidence Intervals For A Mean
300 hundred eggs were randomly chosen from a gravid female salmon and individually weighed. The mean weight was 0.978 g with a standard deviation of 0.042. Find the 95% confidence interval for the mean weight of the salmon eggs (because it is a large n, use the standard normal distribution).
Because we have such a large sample size, we are using the standard normal or z-distribution to calculate the confidence interval.
Formula:


We must find the appropriate z-value based on the given 
Then, find the associated z-score using the z-table for
Now we fill in the formula with our values from the problem to find the 95% CI.
Example Question #1 : How To Find Confidence Intervals For A Mean
A sample of 
Find the 
Because we are only given the sample standard deviation we will use the t-distribution to calculate the confidence interval.
Appropriate Formula:
Now we must identify our variables:
We must find the appropriate t-value based on the given
t-value at 90% confidence:
Look up t-value for 0.05, 55 , so t-value= ~ 1.6735
90% CI becomes:
Example Question #1 : Confidence Intervals
|
Subject |
Horn Length (in) |
Subject |
Horn Length (in) |
|
1 |
19.1 |
11 |
11.6 |
|
2 |
14.7 |
12 |
18.5 |
|
3 |
10.2 |
13 |
28.7 |
|
4 |
16.1 |
14 |
15.3 |
|
5 |
13.9 |
15 |
13.5 |
|
6 |
12.0 |
16 |
7.7 |
|
7 |
20.7 |
17 |
17.2 |
|
8 |
8.6 |
18 |
19.0 |
|
9 |
24.2 |
19 |
20.9 |
|
10 |
17.3 |
20 |
21.3 |
The data above represents measurements of the horn lengths of African water buffalo that were raised on calcium supplements. Construct a 95% confidence interval for the population mean for horn length after supplments.
First you must calculate the sample mean and sample standard deviation of the sample.
Because we do not know the population standard deviation we will use the t-distribution to calculate the confidence intervals. We must use standard error in this formula because we are working with the standard deviation of the sampling distribution.
Formula:
To find the appropriate t-value for 95% confidence interval:
Look up 
Thus the 95% confidence interval is:
Example Question #1 : Confidence Intervals And Mean
The population standard deviation is 7. Our sample size is 36.
What is the 95% margin of error for:
1) the population mean
2) the sample mean
1) 14.567
2) 4.445
1) 15.554
2) 3.656
1) 13.720
2) 2.287
1) 11
2) 3
1) 12.266
2) 3.711
1) 13.720
2) 2.287
For 95% confidence, Z = 1.96.
1) The population M.O.E. =

2) The sample standard deviation =
The sample M.O.E. =
Example Question #1 : Confidence Intervals
The 

What does the confidence interval tell us about the difference in the two programs?
Zero is not in the interval, so reject the null. This is evidence that one program is significantly better at reducing mile times.
The mean improvement of 

Zero is in the interval, so do not reject the null. There is no evidence that one program is better than the other.


The confidence interval is large, so one program is clearly better at reducing mile times than the other.
Zero is in the interval, so do not reject the null. There is no evidence that one program is better than the other.
For there to be a statistically significant difference in the training programs, the 95% confidence interval cannot include zero. 
Example Question #8 : Confidence Intervals
Example Question #9 : Confidence Intervals
Example Question #1 : Confidence Intervals
In a simple random sample of 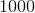


The sample is not sufficiently large. A confidence interval cannot be used.
Step 1: Determine the approporiate formula. In this case, the statistic is a proportion because the question says 261 people out of 1000 are left-handed. We want to use a confidence interval for proportions. The equation is
Step 2: 
Step 3: The questions asks for a 95% confidence interval. You can assume a normal distribution because of the large sample size. Therefore, in a normal distribution, 95% of the data is contained within 
Step 4: Substitue all the values into the equation to get the answer.
Certified Tutor
All AP Statistics Resources




























































