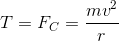All AP Physics C: Mechanics Resources
Example Questions
Example Question #46 : Ap Physics C

A ball of mass 


None of these
This is a centripetal force problem. In this case the tension on the rope is the centripetal force that keeps the ball moving on a circle.
If we want for the rope not to break, then the tension should never exceed 
Now we just solve for velocity:
Example Question #151 : Mechanics Exam
A 1.6kg ball is attached to a 1.8m string and is swinging in circular motion horizontally at the string's full length. If the string can withstand a tension force of 87N, what is the maximum speed the ball can travel without the string breaking?
The ball is experiencing centripetal force so that it can travel in a circular path. This centripetal force is written as the equation below.

Remember that centripetal acceleration is given by the following equation.
Since the centripetal force is coming from the tension of the string, set the tension force equal to the centripetal force.
Since we're trying to find the speed of the ball, we solve for v.
We know the following information from the question.
We can use this information in our equation to solve for the speed of the ball.
Example Question #1 : Circular Motion
In uniform circular motion, the net force is always directed ___________.
away from the center of the circle
nowhere; the net force will be zero
in the same direction as the tangential velocity
toward the center of the circle
toward the center of the circle
The correct answer is "toward the center of the circle." Newton's second law tells us that the direction of the net force will be the same as the direction of the acceleration of the object.
In uniform circular motion, the object accelerates towards the center of the circle (centripetal acceleration); the net force acts in the same direction.
Example Question #1 : Circular Motion
A car moves around a circular path of radius 100m at a velocity of 
The force of friction is what keeps the car in circular motion, preventing it from flying off the track. In other words, the frictional force will be equal to the centripetal force.
We can cancel mass from either side of the equation and rearrange to solve for the coefficient of friction:
We can use our given values to solve:
Example Question #232 : Ap Physics C
An object of mass 10kg undergoes uniform circular motion with a constant velocity of 
The time for one full revolution can be calculated simply by manipulating the defintion of velocity, where the distance is just the circumference of the circlular path. The time it takes is modeled by the following equation:
Use the given radius and velocity to solve for the time per revolution:
Certified Tutor
Certified Tutor
All AP Physics C: Mechanics Resources