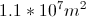Electric Circuits
Help Questions
AP Physics C: Electricity and Magnetism › Electric Circuits
If two identical parallel plate capacitors of capacitance 

Explanation
Relevant equations:
Use the series equation, replacing C1 and C2 with the given constant C:
This agrees with the general rule that the equivalent capacitance in series is less than the capacitance of any of the individual capacitors.
If two identical parallel plate capacitors of capacitance 

Explanation
Relevant equations:
Use the series equation, replacing C1 and C2 with the given constant C:
This agrees with the general rule that the equivalent capacitance in series is less than the capacitance of any of the individual capacitors.
If two identical parallel plate capacitors of capacitance 

Explanation
Relevant equations:
Use the series equation, replacing C1 and C2 with the given constant C:
This agrees with the general rule that the equivalent capacitance in series is less than the capacitance of any of the individual capacitors.
Two parallel conducting plates each have an area of 




Explanation
Relevant equations:
According to the work-energy theorem, work done on the proton is equal to its change in kinetic energy.
1. Find an expression for potential difference, 


2. Multiply the potential difference times the proton charge to find work (and thus kinetic energy):
Two parallel conducting plates each have an area of 




Explanation
Relevant equations:
According to the work-energy theorem, work done on the proton is equal to its change in kinetic energy.
1. Find an expression for potential difference, 


2. Multiply the potential difference times the proton charge to find work (and thus kinetic energy):
Two parallel conducting plates each have an area of 




Explanation
Relevant equations:
According to the work-energy theorem, work done on the proton is equal to its change in kinetic energy.
1. Find an expression for potential difference, 


2. Multiply the potential difference times the proton charge to find work (and thus kinetic energy):
Charge is distributed uniformly over the area of the two plates of a parallel plate capacitor, resulting in a surface area charge density of 




Which of the following would not result in an increase in the measure of electric potential difference between the two plates?
Increase the area, 
Increase the value of the surface charge density, 
Increase the distance, 
Replace the material between the two plates with one of a lower dielectric constant,
Explanation
The electric potential difference created between the plates of a parallel plate capactor is given by the equation:
The charge can be calculated by using the equation:
The value of the capacitance is related to the dimensions of the capacitor with the equation:
Combining these equations yields:
The area becomes inconsequential, while the potential is directly proportional to the surface charge density and the distance between the plates, and inversely proportional to the dielectric of the material between the plates. Changing the area does not cause any change in the potential difference measured between the plates, and changing any of the other variables would cause a resultant change in the potential difference.
A parallel plate capacitor has a capacitance of 

Explanation
The relationship between capacitance, distance, and area is 
Now, we can use the values given in teh question to solve.
A parallel plate capacitor has a capacitance of 

Explanation
The relationship between capacitance, distance, and area is 
Now, we can use the values given in teh question to solve.
Charge is distributed uniformly over the area of the two plates of a parallel plate capacitor, resulting in a surface area charge density of 




Which of the following would not result in an increase in the measure of electric potential difference between the two plates?
Increase the area, 
Increase the value of the surface charge density, 
Increase the distance, 
Replace the material between the two plates with one of a lower dielectric constant,
Explanation
The electric potential difference created between the plates of a parallel plate capactor is given by the equation:
The charge can be calculated by using the equation:
The value of the capacitance is related to the dimensions of the capacitor with the equation:
Combining these equations yields:
The area becomes inconsequential, while the potential is directly proportional to the surface charge density and the distance between the plates, and inversely proportional to the dielectric of the material between the plates. Changing the area does not cause any change in the potential difference measured between the plates, and changing any of the other variables would cause a resultant change in the potential difference.