Newton's Second Law
Help Questions
AP Physics 1 › Newton's Second Law
A man is rolling a recycling bin of mass 


Explanation
Since we are neglecting air resistance, there are two forces in play: gravity and friction. Therefore, we can use Newton's second law to write the following:
Substituting in an expression for the force of gravity and rearranging for the force of friction, we get:
A 


Explanation
We begin by drawing a free body diagram of the block.










To find the force due to friction, we need to find 
Newton's second law is 



There are two forces in the y-direction, 



Substituting all this information into Newton's second law gives us
Assuming 
Now that we have 

We now apply Newton's second law in the direction of acceleration. In this problem, that is the x-direction.
There are two forces in the direction of acceleration,the applied force 






A 


Explanation
We begin by drawing a free body diagram of the block.










To find the force due to friction, we need to find 
Newton's second law is 



There are two forces in the y-direction, 



Substituting all this information into Newton's second law gives us
Assuming 
Now that we have 


We now apply Newton's second law in the direction of acceleration. In this problem, that is the x-direction.
There are two forces in the direction of acceleration, the applied force 






A 

Explanation
We begin by drawing a free body diagram of the block.







Since the block is on ice, there is no friction.
We now apply Newton's second law in the direction of acceleration. In this problem, that is the x-direction.
Newton's second law is 



Solving for mass, we have
The only force in the direction of acceleration is the applied force 


A 

Explanation
We begin by drawing a free body diagram of the block.







Since the block is on ice, there is no friction.
We now apply Newton's second law in the direction of acceleration. In this problem, that is the x-direction.
Newton's second law is 



Solving for acceleration, we have
The only force in the direction of acceleration is the applied force 


A 


Explanation
We begin by drawing a free body diagram of the block.








Newton's second law is 



We now apply Newton's second law in the direction of acceleration. In this problem, that is the x-direction.
Solving for mass, we have
There are two forces in the direction of acceleration,the applied force 





A 


Explanation
The only forces acting on the helicopter are the upward mechanical force and gravity. Newton's second law gives that the net force can be given by 

Using kinematics, we can find the time the helicopter is airborne. Using this kinematic equation 

John has just finished chopping a bunch of firewood and has to get it in a pile by his house. He elects to use a sled to pull the wood across the gravel road to his house. The road and the sled maintain a coefficient of static friction determined to be 


No, he would need 
Yes, the 
No, he would need 
No, he would need 
Explanation
The sled and wood has a mass of
Plug ina and solve.
Use the equation for static friction.
Plug in and solve for the static frictional force.
John will not be able to move the sled and would have to double his efforts to move it.
A truck is pulling a trailer and is accelerating at 







Explanation
The mass of the truck is irrelevant to this problem.
The trailer has a mass of 

This is the force the truck is applying to the trailer to accelerate it forward. Based on Newton's Laws, the trailer is applying the same force, in the opposite direction.
Consider the following system:
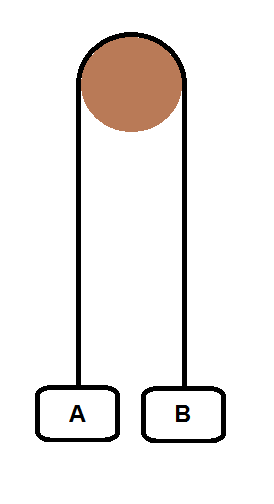
Two masses, A and B, are attached to the end of a rope that runs through a pulley.
The system is at rest. The pulley has become quit old and has develop a thick coat of rust. If 

Explanation
We will approach this problem by looking at the pulley. There are 3 forces applied to the pulley, tension from each weight as well as its internal friction force. To clarify, we will denote that forces in the counterclockwise direction will be positive and forces in the clockwise direction are negative. Also, we need to remember that the internal static friction can be applied in both the clockwise and counterclockwise direction. This will create 2 scenarios. Let's first began when friction is applied in the counter clockwise direction. We will start with Newton's 2nd law:
Since we are asked to find when the system remains at rest, that means the net force on the system is 0:
Now we can begin looking at the three forces. First, we have tension created from mass A. This will be positive since it is in the counterclockwise direction relative to the pulley:
Next we have mass B which will be negative since it's in the opposite direction:
Lastly we have static friction which is positive in this scenario:
Now adding these together to get equation (1):
Rearranging for mass B:
Note that anything greater will result in the system moving.
Now moving onto the 2nd scenario. Let's just jump back to equation (1) and simply reverse the direction of static friction:
Note that anything less than this will result in the system moving. Therefore, the range of mass B that will keep the system stationary is:


















































































