All AP Physics 1 Resources
Example Questions
Example Question #31 : Fundamentals Of Force And Newton's Laws
Suppose that an astronaut on the moon applies a horizontal force of 


In this question, we're told that a horizontal force is being applied to an object on the moon. We're given the magnitude of this force and the mass of the object.
We're also given the acceleration due to gravity on the moon, but this is useless information for the purposes of this question. Since the force under consideration is acting horizontally on the object, and the force due to gravity acts vertically, these two forces are treated separately; the vertical acting force of gravity will not affect the horizontal kinematics of the object's movement.
Thus, this reduces to a simple application of Newton's second law, and we can use the following equation:
Rearranging, we can isolate the term for acceleration:
Then plug in the values that we have to solve for our answer:
Example Question #32 : Fundamentals Of Force And Newton's Laws
Consider the following system:

Two spherical masses, A and B, are attached to the end of a rigid rod with length l. The rod is attached to a fixed point, p, which is at a height, h, above the ground. The rod spins around the fixed point in a vertical circle that is traced in grey. 

The rod is initially at rest and held in the horizontal position. When it is released, what is the initial instantaneous acceleration of mass A, and in what direction? Assume the rod has a negligible mass. Neglect air resistance and internal frictional forces.
None of the other answers
This problem can be solved using the expression relating torque and angular acceleration:
We can determine the total net torque on the system using the Newton's second law.
Applying this to both masses and assuming a force in the downward direction is positive, we get:
Then using the expression for torque, we get:
Where d is half the length of the rod.
Applying this to both masses and assuming torque in the counterclockwise direction is positive, we get:
Now let's go back to the original equation:
Now we need to calculate the net moment of inertia:
Where r is half the length of the rod:
Going back to the original equation and rearranging for angular acceleration:
Then relating this to linear acceleration using:
Where r is half the length of the rod again:
We have all of our values, so we can calculate the final answer:
Example Question #41 : Fundamentals Of Force And Newton's Laws
Consider the following system:
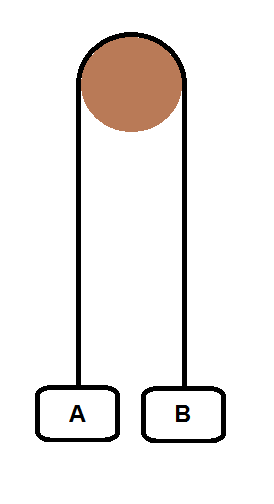
Two masses, A and B, are attached to the end of a rope that runs through a frictionless pulley.
The two masses are initially held at rest. When they are released, what is the initial instantaneous acceleration of mass A, and in what direction? Neglect air resistance and any frictional forces.

We can use Newton's second law:
There are two forces acting on the system: gravity on each mass. For simplicity sake, we will examine these forces with respect to mass. Therefore, the force on mass B becomes an upward tension force on mass A. Now we need to clarify which direction is positive. For this problem, we'll say that a downward force is positive, and an upward force is negative.
We'll start with the gravitational force:
Now for tension. The tension force is simply the gravitational force applied to mass B:
Note that it's negative because it is in the upward direction
Now adding these together to get the net force:
Substituting this back into the original equation, we get:
Where m is the combination of both masses:
Rearrange for acceleration:
We know each value, so we can solve the problem
Example Question #831 : Newtonian Mechanics
Consider the following system:

Two masses, A and B, are attached to the end of a rope that runs through a frictionless pulley.
The two masses are initially at rest. The pulley has a radius 

In order to determine rotational velocity of the pulley, we need the linear velocity of the outside of the pulley, which is simply the linear velocity of the rope/masses. We can determine that using the acceleration of the masses and the length of time given. Therefore, we will begin with Newton's 2nd law applied to one of the two masses. We will arbitrarily apply it to mass A:
There are two forces applied to mass A, gravity and tension from the rope. We will assume that a downward force is positive, and an upward force is negative. First, let's start with gravity:
Next we have tension, which is just the gravitational force applied on mass B:
Adding these together to get net force:
Substituting this into the original equation:
Rearranging for acceleration:
Now that we have acceleration, we can use it to determine linear velocity after the stated length of time:
Now we can use this to determine rotational velocity:
We know all of these values, so time to plug and chug:
Example Question #832 : Newtonian Mechanics
Consider the following system:

Two masses, A and B, are attached to the end of a rope that runs through a pulley.
The system is at rest. The pulley has become quit old and has develop a thick coat of rust. If 

We will approach this problem by looking at the pulley. There are 3 forces applied to the pulley, tension from each weight as well as its internal friction force. To clarify, we will denote that forces in the counterclockwise direction will be positive and forces in the clockwise direction are negative. Also, we need to remember that the internal static friction can be applied in both the clockwise and counterclockwise direction. This will create 2 scenarios. Let's first began when friction is applied in the counter clockwise direction. We will start with Newton's 2nd law:
Since we are asked to find when the system remains at rest, that means the net force on the system is 0:
Now we can begin looking at the three forces. First, we have tension created from mass A. This will be positive since it is in the counterclockwise direction relative to the pulley:
Next we have mass B which will be negative since it's in the opposite direction:
Lastly we have static friction which is positive in this scenario:
Now adding these together to get equation (1):
Rearranging for mass B:
Note that anything greater will result in the system moving.
Now moving onto the 2nd scenario. Let's just jump back to equation (1) and simply reverse the direction of static friction:
Note that anything less than this will result in the system moving. Therefore, the range of mass B that will keep the system stationary is:
Example Question #871 : Ap Physics 1
In a match of tug of war, the Red Team can pull in the positive x-direction with a combined force of 

We will use the sum of forces to solve this equation.
The Red Team will win this match of tug of war by pulling with 
Example Question #43 : Fundamentals Of Force And Newton's Laws
What is the net force required to accelerate a race car that weighs 


To solve this question use Newton's second law and the sum of forces to solve. First, before we solve we have to get our given values into the proper units.
Now we have to solve for the sport car's acceleration
Now use the net forces to solve.

Example Question #44 : Fundamentals Of Force And Newton's Laws
In an experiment on the Moon, the acceleration due to gravity was determined to be 

Looking at the equation for weight. Notice, weight and acceleration are directly proportional. Thus what happens to the acceleration also happens to the weight.
The acceleration due to gravity on the Moon is 
The ball will weigh 
Example Question #45 : Fundamentals Of Force And Newton's Laws
If a toy car with a mass of 


Use Newton's second law to determine the car's acceleration.
Now use a kinematic equation to solve for the time required.
Example Question #46 : Fundamentals Of Force And Newton's Laws
Tony applies a constant horizontal force of 


The bag is on a flat surface, thus the normal force is equal to the weight of the bag.
Use the equation for kinetic friction to solve for the kinetic friction.
Now use the sum of forces to solve for the net force acting on the bag.
There will be a total of 
Certified Tutor
All AP Physics 1 Resources












































































































































