Specific Forces
Help Questions
AP Physics 1 › Specific Forces
Two asteroids in space are in close proximity to each other. Each has a mass of 

Explanation
To solve this problem, use Newton's law of universal gravitation:
We are given the constant, as well as the asteroid masses and distance (radius). Using these values we can solve for the force.
A man pulls a 



We must know the mass of the box to solve
Explanation
Work is equal to the change in energy of the system. We are given the weight of the box and the vertical displacement, which will allow us to calculate the change in potential energy. This will be the total work required to move the box against gravity.
The remaining work that the man exerts must have been used to counter the force of friction acting against his motion.
Now we know the work performed by friction. Using this value, we can work to solve for the force of friction and the coefficient of friction. First, we will need to use a second formula for work:
In this case, the distance will be the distance traveled along the surface of the incline. We can solve for this distance using trigonometry.
We know the work done by friction and the distance traveled along the incline, allowing us to solve for the force of friction.
Finally, use the formula for frictional force to solve for the coefficient of friction. Keep in mind that the force on the box due to gravity will be equal to 
Plug in our final values and solve for the coefficient of friction.
Two asteroids in space are in close proximity to each other. Each has a mass of 

Explanation
To solve this problem, use Newton's law of universal gravitation:
We are given the constant, as well as the asteroid masses and distance (radius). Using these values we can solve for the force.
An astronaut is in orbit around the earth. The feeling of weightlessness that he experiences is due to the absence of which force?
Normal force
Gravitational force
Frictional force
Buoyant force
Explanation
The correct answer is normal force. Normal force will occur when the astronaut is standing on a surface, which will push back on him. Gravity is present since the astronaut is in orbit (gravity provides the centripetal force). The feeling of weightlessness he experiences is due to the absence of a surface to push back on him/her.
Nicola is attempting to create a single tiered mobile as shown. She has a wooden dowel (




If Nicola places ornament 



Note: figure not drawn to scale.




Explanation
Let's use the midpoint as our point of reference. With that said, 



Our main equation is this:
Where 


Now let's plug in our numbers, remember about our negative/positive sides!
This should give us
Now, because this number is negative, we know it's to the left of our midpoint (if you chose to set up your -/+ sides opposite of how we did it, your answer will be positive). Regardless of the outcome, this measurement is meant to be taken from object A to the midpoint. Well, do any of our answers have either (+) or (-) 

One side is

Think about it logically too (use your pencil). The heavier end of a pencil usually has a bulky eraser on it (just like the bulkier object on the left). Try holding the pencil at the tip's end, and then gradually try balancing it in the same manner as you move closer to the eraser.
ALSO NOTE: the question states the weight of the dowel as well. But look we didn't even need it. Sometimes the AP exam will give you some aspects in the question to distract you.
Suppose that a student pushes his physics textbook across the table with his hand. In doing so, what type of force is acting on the book?
Electromagnetic force
Gravitational force
Strong force
Weak force
Explanation
If a person were to use their hand to push a book across the table, the type of force that their hand is applying to the book is classified as an electromagnetic force. Even though this may not seem intuitive, the reason is that the electrostatic repulsion of the atoms in the person's hand repel the atoms in the book. Due to this electrostatic repulsion between the atoms in the person's hand and the atoms in the book, the force is electromagnetic.
Gravitational forces occur due to gravity, that is, from an attraction between any two objects with mass. The strong and weak forces are both nuclear forces that act only across very, very short distances. Generally, these forces are only significant at the sub-atomic level in the atom's nucleus, and thus do not have a role at greater distances (such as between the person's hand and the book).
Mass of Mars:
Universal gravitation constant:
Radius of Mars:
A buggy on the surface of Mars locks up it's break and slides on Martian ice. If the buggy was traveling at 

None of these
Explanation
The normal force will be equal to the magnitude of the force of gravity pushing the buggy into the ground.
Using definition of frictional force and work equation:
Combining equations:
Canceling out the mass of the buggy and plugging in values:
Solving for
Consider the following system:
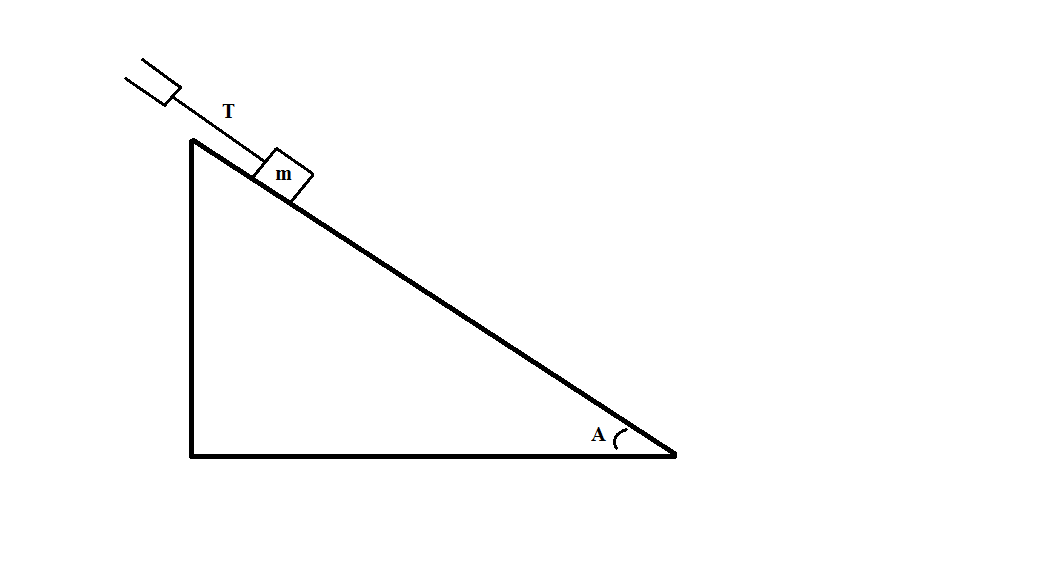
If the mass is 


Explanation
Since there is no friction between the mass and slope, there are only two relevant forces acting on the mass: gravity and tension. Furthermore, since the block is not in motion, we know that these forces are equal to each other. Therefore:
Substituting in an expression for the force of gravity, we get:
We know all of these values, allowing us to solve for the tension:
A man pulls a 



We must know the mass of the box to solve
Explanation
Work is equal to the change in energy of the system. We are given the weight of the box and the vertical displacement, which will allow us to calculate the change in potential energy. This will be the total work required to move the box against gravity.
The remaining work that the man exerts must have been used to counter the force of friction acting against his motion.
Now we know the work performed by friction. Using this value, we can work to solve for the force of friction and the coefficient of friction. First, we will need to use a second formula for work:
In this case, the distance will be the distance traveled along the surface of the incline. We can solve for this distance using trigonometry.
We know the work done by friction and the distance traveled along the incline, allowing us to solve for the force of friction.
Finally, use the formula for frictional force to solve for the coefficient of friction. Keep in mind that the force on the box due to gravity will be equal to 
Plug in our final values and solve for the coefficient of friction.
Consider the following system:

If the mass is 


Explanation
Since there is no friction between the mass and slope, there are only two relevant forces acting on the mass: gravity and tension. Furthermore, since the block is not in motion, we know that these forces are equal to each other. Therefore:
Substituting in an expression for the force of gravity, we get:
We know all of these values, allowing us to solve for the tension:

























































