All AP Calculus AB Resources
Example Questions
Example Question #1 : Derivative Rules For Sums, Products, And Quotients Of Functions
Find the derivative of the function,
Differentiate both sides and proceed with the product rule:
![\frac{dy}{dx}=\frac{d}{dx}[x^2\sin(3x)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/749291/gif.latex)
Evaluate the derivatives in each term. For the first term,

apply the chain rule,
So now the first term in equation (2) can be written,
![x^2\frac{d}{dx}\sin(3x)=x^2[3\cos(3x)]=3x^2\cos(3x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741374/gif.latex)
The second term in equation (2) is easy, this is just the product of 


Combine equations (3) and (4) to write the derivative,
Example Question #201 : Computation Of The Derivative
Find the derivative.
Use the product rule to find the derivative.
Example Question #3 : Derivative Rules For Sums, Products, And Quotients Of Functions
Find the derivative.
Use the power rule to find the derivative.
Thus, the derivative is
Example Question #4 : Derivative Rules For Sums, Products, And Quotients Of Functions
Find 
Here we use the product rule:
Let 
Then 
and 
Subbing these values back into our equation gives us
Simplify by combining like-terms
and pulling out a 
Example Question #5 : Derivative Rules For Sums, Products, And Quotients Of Functions
If 

When evaluating the derivative, pay attention to the fact that 

and hence

Example Question #6 : Derivative Rules For Sums, Products, And Quotients Of Functions
If 
To obtain an expression for 


Substituting 

Example Question #2 : Derivative Rules For Sums, Products, And Quotients Of Functions
If 

To find 






Example Question #8 : Derivative Rules For Sums, Products, And Quotients Of Functions
Find the derivative of the following equation:
None of the other answers
Because this problem contains two functions multiplied together that can't be simplified any further, it calls for the product rule, which states that 
By using this rule, we get the answer:
By simplifying, we conclude that the derivative is equal to

Example Question #9 : Derivative Rules For Sums, Products, And Quotients Of Functions
Example Question #10 : Derivative Rules For Sums, Products, And Quotients Of Functions
Certified Tutor
All AP Calculus AB Resources




![\frac{dy}{dx} =x[3x\cos(3x)+2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741367/gif.latex)

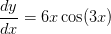


























































![\begin{align*}&\text{The function that we have been given can be seen as two smaller functions}\\&\text{multiplied together, the first being: }cos(19x)\\&\text{and the second being: }\frac{1}{x^{20}}\\&\text{With the product scaled by }-114\\&\text{To perform the derivative, }\text{ we'll wish to use the product rule, }d[uv]=udv+vdu\\&\text{along with the following:}\\&d[cos(ax)]=-asin(ax)dx\\&d[x^a]=ax^{a-1}dx\\&\text{From the above we can continue:}\\&u=cos(19x);du=-19sin(19x)\\&v=\frac{1}{x^{20}};dv=-\frac{20}{x^{21}}\\&\text{We can then combine these terms (Don't forget the scalar!)}\\&\text{So the derivative is:}\\&\frac{(2280cos(19x))}{x^{21}}+\frac{ (2166sin(19x))}{x^{20}}\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/923697/gif.latex)





![\begin{align*}&\text{The function that we have been given can be seen as two smaller functions}\\&\text{multiplied together, the first being: }tan(17x)\\&\text{and the second being: }\frac{1}{2^{(20x)}}\\&\text{With the product scaled by }-380\\&\text{To perform the derivative, }\text{ we'll wish to use the product rule, }d[uv]=udv+vdu\\&\text{along with the following:}\\&d[tan(ax)]=\frac{adx}{cos^2(ax)}=(atan^2(ax)+a)dx\\&d[b^{ax}]=ab^{ax}ln(b)sx\\&\text{From the above we can continue:}\\&u=tan(17x);du=17tan(17x)^{2} + 17\\&v=\frac{1}{2^{(20x)}};dv=-\frac{(20ln(2))}{2^{(20x)}}\\&\text{We can then combine these terms (Don't forget the scalar!)}\\&\text{So the derivative is:}\\&\frac{(7600tan(17x)ln(2))}{2^{(20x)}}-\frac{ (380\cdot (17tan(17x)^{2} + 17))}{2^{(20x)}}\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/923677/gif.latex)



