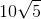Graphing Circle Functions
Help Questions
Algebra II › Graphing Circle Functions
What are the coordinates of the center of a circle with the equation 
Explanation
The equation of a circle is 
What is the radius of a circle with the equation 
Explanation
To convert the given equation into the format 

The square root of 4 is 2, so the radius of the circle is 2.
Give the radius and the center of the circle for the equation below.
Explanation
Look at the formula for the equation of a circle below.
Here 




Which equation does this graph represent?

Explanation
The equation of a circle is 
Which equation does this graph represent?

Explanation
The equation of a circle is 
What is the radius of a circle with the equation 
Explanation
To convert the given equation into the format 

The square root of 25 is 5, so the radius of the circle is 5.
Determine the graph of the equation
Circle, centered at 
Ellipse, centered at
Circle, centered at 
Hyperbola, centered at
Explanation
The equation of a circle in standard for is:
Where the center 

Dividing by 4 on both sides of the equation yields
or
an equation whose graph is a circle, centered at (2,3) with radius = .5
The graph of the equation
is a circle with what as the length of its radius?
Explanation
Rewrite the equation of the circle in standard form
as follows:
Since 

The standard form of the equation sets

so the radius of the circle is
What is the center of the circle expressed by the funciton 
Explanation
The equation can be rewritten so that it looks like the parent equation for a circle 




What is the radius of the circle?
Explanation
The parent equation of a circle is represented by