All Algebra 1 Resources
Example Questions
Example Question #1 : Writing Inequalities
Write a compound inequality that describes the given graph: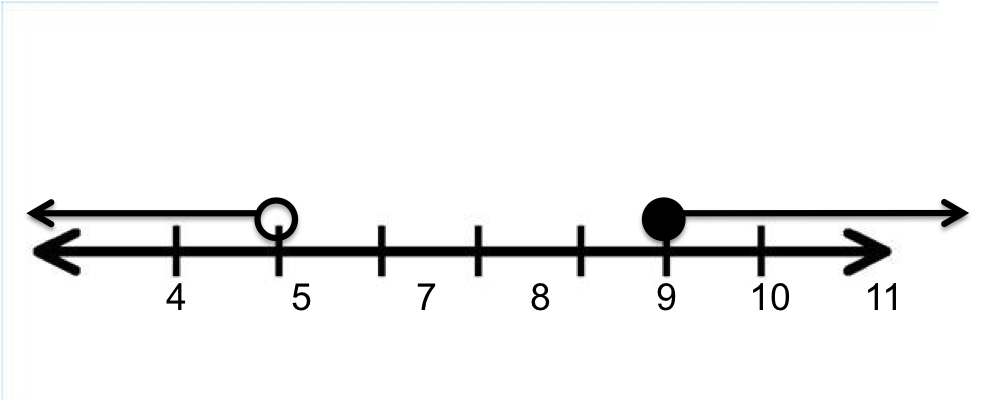
The graph shows an arrow beginning on 5 with an open circle and pointing to the left, thus that portion of the graph says, all real numbers less than 5. There is a second arrow beginning on 9 with a closed circle and pointing to the right, representing all real numbers greater than or equal to 9. Since we are joining the two parts of the graph, we have a compound inequality utilizing the "or" statement. So our answer is 
Example Question #2 : Writing Inequalities
Write as an algebraic inequality:
Twenty subtracted from the product of seven and a number exceeds one hundred.
"The product of seven and a number " is 

Example Question #3 : Writing Inequalities
Write as an algebraic inequality:
Twice the sum of a number and sixteen is no less than sixty.
"The sum of a number and sixteen" is translates to 


Example Question #3 : Writing Inequalities
Write as an algebraic inequality:
Twice the sum of a number and sixteen does not exceed eighty.

"The sum of a number and sixteen" translates to 

Example Question #1 : Writing Inequalities
A candy company is inspecting its factory. In a standard bag of candy there are a minimum of 14 individual candies, and a maximum of 22. Let 

In terms of inequalities, we know two things. 



So, we have to find the correct statement where we can find the two inequalities. We see we need 

Therefore the only answer that fits our needs is 
Example Question #1 : Writing Inequalities
Write an inequality that represents the following number line.
![]()

On the number line, the graph starts at –1 and ends at 3.
The line runs between –1 and 3, so we know our inequality involves only values of x that fall between these two numbers. The open circle at –1 indicates that –1 is not included, while the shaded circle on 3 indicates that 3 is included.
Combining these two inequalities into one give us our answer.
Example Question #2 : Writing Inequalities
Find the solution set of the inequality:
or, in interval notation,
Example Question #1 : Writing Inequalities
Find the solution set of the inequality:
or, in interval notation,
Example Question #2 : Writing Inequalities
Solve for 
The first step is to distribute (multiply) through the parentheses:
Then subtract 
Next, subtract the 12:
Finally, divide by two:
Example Question #3 : Writing Inequalities
Solve the inequality.
To solve 
Subtract 

Divide by nine on both sides.
This answer is also the same as:
All Algebra 1 Resources







































![(-\infty , -12.5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/48301/gif.latex)
![(-\infty , 12.5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/48300/gif.latex)





![(-\infty , 12.5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93144/gif.latex)



































