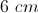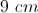Isosceles Triangles
Help Questions
ACT Math › Isosceles Triangles
Find the hypotenuse of an isosceles right triangle given side length of 3.
Explanation
To solve, simply use the Pythagorean Theorem.
Recall that an isosceles right triangle has two leg lengths that are equal.
Therefore, to solve for the hypotenuse let 

Thus,
Find the hypotenuse of an isosceles right triangle given side length of 3.
Explanation
To solve, simply use the Pythagorean Theorem.
Recall that an isosceles right triangle has two leg lengths that are equal.
Therefore, to solve for the hypotenuse let 

Thus,
Find the hypotenuse of an isosceles right triangle given side length of 3.
Explanation
To solve, simply use the Pythagorean Theorem.
Recall that an isosceles right triangle has two leg lengths that are equal.
Therefore, to solve for the hypotenuse let 

Thus,
What is the height of an isosceles triangle which has a base of 

Explanation
The area of a triangle is given by the equation:
In this case, we are given the area (


To do this, we must plug in the given values for 

We then must multiply the right side, and then divide the entire equation by 2, in order to solve for 
Therefore, the height of the triangle is 
What is the height of an isosceles triangle which has a base of 

Explanation
The area of a triangle is given by the equation:
In this case, we are given the area (


To do this, we must plug in the given values for 

We then must multiply the right side, and then divide the entire equation by 2, in order to solve for 
Therefore, the height of the triangle is 
What is the height of an isosceles triangle which has a base of 

Explanation
The area of a triangle is given by the equation:
In this case, we are given the area (


To do this, we must plug in the given values for 

We then must multiply the right side, and then divide the entire equation by 2, in order to solve for 
Therefore, the height of the triangle is 
The base angle of an isosceles triangle is thirteen more than three times the vertex angle. What is the difference between the vertex angle and the base angle?
Explanation
Every triangle has 
Let 

The equation to solve becomes 
Now we can solve for the vertex angle.
The difference between the vertex angle and the base angle is 
The base angle of an isosceles triangle is thirteen more than three times the vertex angle. What is the difference between the vertex angle and the base angle?
Explanation
Every triangle has 
Let 

The equation to solve becomes 
Now we can solve for the vertex angle.
The difference between the vertex angle and the base angle is 
The base angle of an isosceles triangle is thirteen more than three times the vertex angle. What is the difference between the vertex angle and the base angle?
Explanation
Every triangle has 
Let 

The equation to solve becomes 
Now we can solve for the vertex angle.
The difference between the vertex angle and the base angle is 
An isosceles triangle has a base of 

Explanation