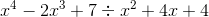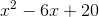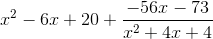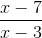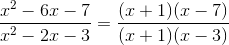How to divide trinomials
Help Questions
ACT Math › How to divide trinomials
Divide:
Explanation

The set up would look very similar to the division of real numbers, such as when we want to divide 10 by 2 and the answer is 5.
The first step after setting up the "division house" is to see what the first term in the outer trinomial needs to multiplied by to match the 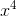


While we could continue to divide, it would require the use of fraction exponents that would make the answer more complicated. Therefore, the term in red will be the remainder. Because this remainder is still subject to be being divided by the trinomial outside of the division house, we will make the remainder part of the final answer by writing it in fraction form:
Therefore the final answer is
Simplify the expression:
Explanation
Once simplified, (x+1) appears on both the numerator and denominator, meaning we can cancel out both of them.
Which gives us: