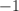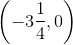All SAT Math Resources
Example Questions
Example Question #11 : How To Find X Or Y Intercept
Find the x-intercepts of 
To find the x-intercepts, plug 

Don't forget that there are two solutions, both negative and positive!
Example Question #12 : How To Find X Or Y Intercept
A line with the exquation 


By plugging in the coordinate, we can figure out that 




Example Question #11 : How To Find X Or Y Intercept
What are the 
We can factor 



Therefore our 


Example Question #211 : Coordinate Geometry
Which of the following lines does not intersect the line 
Parallel lines never intersect, so you are looking for a line that has the same slope as the one given. The slope of the given line is –4, and the slope of the line in y = –4x + 5 is –4 as well. Since these two lines have equal slopes, they will run parallel and can never intersect.
Example Question #212 : Coordinate Geometry
Find the y-intercept of 
12
7
3
5
14
7
To find the y-intercept, set x equal to zero and solve for y.
This gives y = 3(0)2 + 2(0) +7 = 7.
Example Question #16 : How To Find X Or Y Intercept
The slope of a line is 

None of the available answers
The equation for a line is:

We can solve for 
Our line is now
Our x-intercept occurs when 

Example Question #213 : Coordinate Geometry
Determine the x-intercept for the equation:
The x-intercept is the x-value when the value of 

The x-intercept is 
Example Question #213 : Coordinate Geometry
What is the y intercept of
y=12
y=-3
The line does not cross the y axis.
y=3
y=3
To find the y intercept, substitute x=0
Example Question #23 : X And Y Intercept
At what point does the line 
None of the given answers
We know that in slope-intercept form, 

Therefore, when 


Example Question #605 : Sat Mathematics
Give the area of the triangle on the coordinate plane that is bounded by the 


None of the other choices gives the correct response.
It is necessary to find the vertices of the triangle, which can be done by finding the three points at which two of the three lines intersect.
The intersection of the 





The intersection of the 







The intersection of the lines with equations 



Since 


The lines in question are graphed below, and the triangle they bound is shaded:

If we take the vertical side as the base, its length is seen to be 3; the height is the horizontal distance to the opposite vertex, which is its 


Certified Tutor
Certified Tutor
All SAT Math Resources