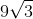How to find the area of a right triangle
Help Questions
SAT Math › How to find the area of a right triangle
The vertices of a right triangle on the coordinate axes are at the origin, 

Explanation
The triangle in question can be drawn as the following:

The lengths of the legs of the triangle are 12, the distance from the origin to 


If the hypotenuse of a triangle is 5 meters, which of the following is the closest value to the area of the triangle?
5
12
26
45
54
Explanation
The answer is 12. In this circumstance, the area of the triangle cannot be smaller than its hypotenuse length, and cannot be bigger than its hypotenuse squared (that would be the area of a square).
A right triangle has a total perimeter of 12, and the length of its hypotenuse is 5. What is the area of this triangle?
3
6
10
12
15
Explanation
The area of a triangle is denoted by the equation 1/2 b x h.
b stands for the length of the base, and h stands for the height.
Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.
So, 12-5 = 7 for the total perimeter of the base and height.
7 does not divide cleanly by two, but it does break down into 3 and 4,
and 1/2 (3x4) yields 6.
Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here
Figure not drawn to scale.
In the figure above, rays PA and PB are tangent to circle O at points A and B, respectively. If the diameter of circle O is 16 units and the length of line segment PO is 17 units, what is the area, in square units, of the quadrilateral PAOB?
60
120
240
136
68
Explanation
Because PA and PB are tangent to circle O, angles PAO and PBO must be right angles; therefore, triangles PAO and PBO are both right triangles.
Since AO and OB are both radii of circle O, they are congruent. Furthermore, because PA and PB are external tangents originating from the same point, they must also be congruent.
So, in triangles PAO and PBO, we have two sides that are congruent, and we have a congruent angle (all right angles are congruent) between them. Therefore, by the Side-Angle-Side (SAS) Theorem of congruency, triangles PAO and PBO are congruent.
Notice that quadrilateral PAOB can be broken up into triangles PAO and PBO. Since those triangles are congruent, each must comprise one half of the area of quadrilateral PAOB. As a result, if we find the area of one of the triangles, we can double it in order to find the area of the quadrilateral.
Let's determine the area of triangle PAO. We have already established that it is a right triangle. We are told that PO, which is the hypotenuse of the triangle, is equal to 17. We are also told that the diameter of circle O is 16, which means that every radius of the circle is 8, because a radius is half the size of a diameter. Since segment AO is a radius, its length must be 8.
So, triangle PAO is a right triangle with a hypotenuse of 17 and a leg of 8. We can use the Pythagorean Theorem in order to find the other leg. According to the Pythagorean Theorem, if a and b are the lengths of the legs of a right triangle, and c is the length of the hypotenuse, then:
a2 + b2 = c2
Let us let b represent the length of PA.
82 + b2 = 172
64 + b2 = 289
Subtract 64 from both sides.
b2 = 225
Take the square root of both sides.
b = 15
This means that the length of PA is 15.
Now let's apply the formula for the area of a right triangle. Because the legs of a right triangle are perpendicular, one can be considered the base, and the other can be considered the height of the triangle.
area of triangle PAO = (1/2)bh
= (1/2)(8)(15) = 60
Ultimately, we must find the area of quadrilateral PAOB; however, we previously determined that triangles PAO and PBO each comprise half of the quadrilateral. Thus, if we double the area of PAO, we would get the area of quadrilateral PAOB.
Area of PAOB = 2(area of PAO)
= 2(60) = 120 square units
The answer is 120.
The perimeter of a right triangle is 40 units. If the lengths of the sides are 


Explanation
Because the perimeter is equal to the sum of the lengths of the three sides of a triangle, we can add the three expressions for the lengths and set them equal to 40.
Perimeter:
Simplify the x terms.
Simplify the constants.
Subtract 8 from both sides.
Divide by 4
One side is 8.
The second side is

The third side is

Thus, the sides of the triangle are 8, 15, and 17.
The question asks us for the area of the triangle, which is given by the formula (1/2)bh. We are told it is a right triangle, so we can use one of the legs as the base, and the other leg as the height, since the legs will intersect at right angles. The legs of the right triangle must be the smallest sides (the longest must be the hypotenuse), which in this case are 8 and 15. So, let's assume that 8 is the base and 15 is the height.
The area of a triangle is (1/2)bh. We can substitute 8 and 15 for b and h.

The answer is 60 units squared.
The length of one leg of an equilateral triangle is 6. What is the area of the triangle?
Explanation
The base is equal to 6.
The height of an quilateral triangle is equal to 

The ratio for the side lengths of a right triangle is 3:4:5. If the perimeter is 48, what is the area of the triangle?
50
48
96
108
240
Explanation
We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.
Triangle ABC is drawn between the points A(4, 3), B(4, 8), and C(7, 3). What is the area of ABC?
Explanation
Drawing a quick sketch of this triangle will reveal that it is a right triangle. The lines AB and AC form the height and base of this triangle interchangeably, depending on how you look at it.
Either way the formula for the area of the triangle is the distance from A to B multiplied by the distance from A to C, divided by 2.
This is

Figure NOT drawn to scale.



Choose the closest answer.
Explanation
The altitude of a right triangle from the vertex of its right angle - which, here, is 


The similarity ratio of 

The ratio of the areas of two similar triangles is the square of their similarity ratio, which here is
Therefore, the area of 
the overall area of