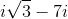Squaring / Square Roots / Radicals
Help Questions
SAT Math › Squaring / Square Roots / Radicals
Simplify the radical expression.
Explanation
Look for perfect cubes within each term. This will allow us to factor out of the radical.
Simplify.
According to Heron's Formula, the area of a triangle with side lengths of a, b, and c is given by the following:
where s is one-half of the triangle's perimeter.
What is the area of a triangle with side lengths of 6, 10, and 12 units?
12√5
4√14
8√14
14√2
48√77
Explanation
We can use Heron's formula to find the area of the triangle. We can let a = 6, b = 10, and c = 12.
In order to find s, we need to find one half of the perimeter. The perimeter is the sum of the lengths of the sides of the triangle.
Perimeter = a + b + c = 6 + 10 + 12 = 28
In order to find s, we must multiply the perimeter by one-half, which would give us (1/2)(28), or 14.
Now that we have a, b, c, and s, we can calculate the area using Heron's formula.
Simplify:
Explanation
If you don't already have the pattern memorized, use FOIL. It's best to write out the parentheses twice (as below) to avoid mistakes:


The correct answer is not listed.
Explanation
This gives us roots of
The product of 
The sum of these 4 is:
What we notice is that each of the roots has a negative. It thus makes sense that they will all cancel out. Rather than going through all the multiplication, we can instead look at the very beginning setup, which we can simplify using the distributive property:
Find the product of (3 + 4i)(4 - 3i) given that i is the square root of negative one.
7 + i
0
12 - 12i
24
24 + 7i
Explanation
Distribute (3 + 4i)(4 - 3i)
3(4) + 3(-3i) + 4i(4) + 4i(-3i)
12 - 9i + 16i -12i2
12 + 7i - 12(-1)
12 + 7i + 12
24 + 7i
Simplify:
Explanation
Rewrite 


The correct answer is not listed.
Explanation
This gives us roots of
The product of 
The sum of these 4 is:
What we notice is that each of the roots has a negative. It thus makes sense that they will all cancel out. Rather than going through all the multiplication, we can instead look at the very beginning setup, which we can simplify using the distributive property:
Define an operation 

If 

Explanation



Rationalize the denominator by multiplying both numerator and denominator by the complex conjugate of the latter, which is 
Simplify:
Explanation
Use FOIL:
Combine like terms:
But since 
Evaluate 
None of the other choices gives the correct response.
Explanation
Apply the Power of a Product Rule:

and

so, substituting and evaluating:
![\sqrt[3]{-64x^{6}y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26625/gif.latex)




![\sqrt[3]{-64}*\sqrt[3]{x^6}*\sqrt[3]{y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/85063/gif.latex)
![\sqrt[3]{-4*-4*-4}*\sqrt[3]{x^2*x^2*x^2}*\sqrt[3]{y^4*y^4*y^4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/119850/gif.latex)



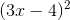

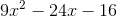


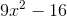


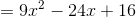










![[(-2+5i) + (2-5i)] + [(5+2i) + (-5-2i)] =](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26403/gif.latex)
![=[(-2)+2 +5i - 5i] + [5-5 + 2i - 2i] = [0] + [0] = 0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26404/gif.latex)
![1(5+2i) + (-1)\cdot(5+2i)+ i(5+2i)+(-i) \cdot(5+2i) = (5+2i)\cdot[1+(-1)+i+(-i)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26405/gif.latex)
![= (5+2i)\cdot[0] = 0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26406/gif.latex)