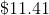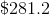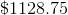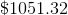All SAT Math Resources
Example Questions
Example Question #1 : How To Find Compound Interest
A five-year bond is opened with 

Each year, you can calculate your interest by multiplying the principle (

For two years, it would be:

Therefore, you can solve for a five year period by doing:
Using your calculator, you can expand the 


Example Question #2 : How To Find Compound Interest
If a cash deposit account is opened with 

It is easiest to break this down into steps. For each year, you will multiply by 
After year 1: 
After year 2: 

After year 3: 

Thus, the positive difference of the interest from the last period and the interest from the first period is:
Example Question #2 : How To Find Compound Interest
Jack has 



First, break the problem into two segments: the amount Jack invests in the high-yield savings, and the amount Jack invests in the simple interest account (10,000 and 5,000 respectively).
Now let's work with the high-yield savings account. $10,000 is invested at an annual rate of 8%, compounded quarterly. We can use the compound interest formula to solve:
Plug in the values given:
Therefore, Jack makes $824.32 off his high-yield savings account. Now let's calculate the other interest:
Add the two together, and we see that Jack makes a total of, 
Example Question #191 : New Sat
A truck was bought for 

The first step is to convert the depreciation rate into a decimal. 




Example Question #1 : Pattern Behaviors In Exponents
If ax·a4 = a12 and (by)3 = b15, what is the value of x - y?
3
6
-4
-2
-9
3
Multiplying like bases means add the exponents, so x+4 = 12, or x = 8.
Raising a power to a power means multiply the exponents, so 3y = 15, or y = 5.
x - y = 8 - 5 = 3.
Example Question #1 : How To Find Patterns In Exponents
If p and q are positive integrers and 27p = 9q, then what is the value of q in terms of p?
3p
(3/2)p
2p
(2/3)p
p
(3/2)p
The first step is to express both sides of the equation with equal bases, in this case 3. The equation becomes 33p = 32q. So then 3p = 2q, and q = (3/2)p is our answer.
Example Question #2 : Pattern Behaviors In Exponents
Simplify 272/3.
729
3
9
125
27
9
272/3 is 27 squared and cube-rooted. We want to pick the easier operation first. Here that is the cube root. To see that, try both operations.
272/3 = (272)1/3 = 7291/3 OR
272/3 = (271/3)2 = 32
Obviously 32 is much easier. Either 32 or 7291/3 will give us the correct answer of 9, but with 32 it is readily apparent.
Example Question #3 : Pattern Behaviors In Exponents
If 


what is the value of 
To solve this problem, we will have to take the log of both sides to bring down our exponents. By doing this, we will get 
To solve for 



Example Question #4 : Pattern Behaviors In Exponents
If


We use two properties of logarithms:
So
Example Question #1 : How To Find Patterns In Exponents
Evaluate:




Certified Tutor
Certified Tutor
All SAT Math Resources