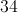All SAT Math Resources
Example Questions
Example Question #211 : Algebra
The Widget Company makes widgets. The monthly fixed costs are $750. It costs $45 to make each widget. The widgets sell for $75 a piece.
What is the monthly break-even point?
The break-even point is where the costs equal revenue.
Let 
Costs:
Revenue:
So the equation to solve becomes
So the break-even point occurs when they sell 25 widgets.
Example Question #41 : Equations / Inequalities
The Widget Company makes widgets. The monthly fixed costs are $750. It costs $45 to make each widget. The widgets sells for $75 a piece.
The Widget Company wants to make a profit of $3,000. How many widgets must be sold?
Profits = Revenues - Costs
Revenue:
Costs:
Profit:
So the equation to solve becomes
So a $3,000 profit occurs when they sell 125 widgets
Example Question #41 : Equations / Inequalities
Sally sells custom picture frames. Her monthly fixed costs are $350. It costs $10 to make each frame. Sally sells her picture frames for $35 each.
To make a profit of $500, how many frames need to be sold?
Let 
Revenues:
Costs:
Profits =
So the equation to solve becomes
So 34 picture frames must be sold to make a $500 profit.
Example Question #43 : Equations / Inequalities
How much pure water must be added to 2 gallons of 90% pure cleaning solution to yield a 30% pure cleaning solution?
Let pure water be 0% and pure solution be 100%.
So the general equation to solve is:



So the equation to solve becomes
Solving shows that we need to add 4 gallons of pure water to 2 gallons of 90% pure cleaning solution to get a 30% pure solution.
Example Question #82 : How To Find The Solution To An Equation
Susan got a new piggy bank and counted the change she put into it. She had one more nickel than dimes and two fewer quarters than nickles. The value of her change was $1.40. How many total coins did she have?
Let 


The general equation to use is:



So the equation to solve becomes
Thus, solving the equation shows that she had five nickels, four dimes, and three quarters giving a total of 12 coins.
Example Question #101 : Equations / Inequalities
How much pure water should be added to 
Pure water is 0% and pure solution is 100%



So the equation to solve becomes
So we need to add 

Example Question #83 : How To Find The Solution To An Equation
Luke purchased a tractor for $1200. The value of the tractor decreases by 25 percent each year. The value, 


In how many years from the date of purchase will the value of the tractor be $675?
5
2
1
3
4
2
We are looking for the value of t that gives $675 as the result when plugged in V (t ). While there are many ways to do this, one of the fastest is to plug in the answer choices as values of t .
When we plug t = 1 into V (t ), we get V (1) = 1200(0.75)1 = 1000(0.75) = $900, which is incorrect.
When we plug t = 2 into V (t ), we get V (2) = 1200(0.75)2 = $675, so this is our solution.
The value of the tractor will be $675 after 2 years.
Finally, we can see that if t = 3, 4, or 5, the resulting values of the V (t ) are all incorrect.
Example Question #84 : How To Find The Solution To An Equation
Solve for 
First combine like terms. In this case, 4x and 9x can be added together:
13x + 13 = 0
Subtract 13 from both sides:
13x = -13
Divide both sides by 13 to isolate x:
x = -13/13
x = -1
Example Question #111 : Equations / Inequalities
Ben is walking three dogs that weigh an average of 75 pounds each. Ben begins to walk a fourth dog, and the average weight of the dogs decreases to 70 pounds. What is the weight in pounds of the fourth dog?
The total weight of the first three dogs is 225 pounds. This amount, plus the weight of the fourth dog, divided by total number of dogs, is the new average weight:
Example Question #86 : How To Find The Solution To An Equation
Pets Plus makes bird houses. Their monthly fixed expenses are $750. The cost for each bird house is $15. The bird houses sell for $40.
What is the monthly break-even point at Pets Plus?
Let 
The break-even point is where the revenue is the same as the costs:


Solve for 
Therefore, Pets Plus must sell 30 bird houses to break-even.
All SAT Math Resources