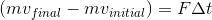All SAT II Physics Resources
Example Questions
Example Question #1 : Mechanics
A model rocket, launched vertically, travels upwards 
The answer cannot be determined from this information
At the highest point of the flight
The acceleration remains constant throughout the flight
Just before landing
Just after launch
The acceleration remains constant throughout the flight
Newton's second law tells us that force and acceleration are directly related; if there is an acceleration, then there is also a force. This principle can help conceptualize this question.
While the rocket is in the air, there is only one force acting on it: the force of gravity. We can thus conclude that the acceleration of the rocket is directly related to this force. Since the force on the rocket (the force of gravity) is constant, its acceleration is also constant.
Any object that is in projectile or free-fall motion will experience a constant acceleration due to gravity.
Example Question #1 : Linear Motion
Which of these is not an example of Newtonian mechanics?
Newtonian mechanics apply to all objects of substantial mass travelling at significantly slower than the speed of light.
Newton's law of universal gravitation, Newton's second law, momentum, and the equation for mechanical energy all fall under Newtonian mechanics.
The mass-energy equivalence suggests that mass can change as the speed of an object (such as an electron) approaches the speed of light. Newtonian mechanics assume that mass is constant, and do not apply to objects approaching the speed of light.
Example Question #1 : Linear Motion Calculations
Near the surface of the earth, a projectile is fired from a canon at an angle of 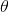

At the maximum height of projectile motion, 


We can then rearrange for
Next substitute this value into the equation 
Example Question #1 : Linear Motion
Sam throws a 



How long is the rock in the air?
We first need to find the vertical component of the velocity.
We can plug in the given values for the angle and the initial velocity to find the vertical component.
Now we need to solve for the time that the rock travels upward. We can then add the upward travel time to the downward travel time to find the total time in the air.
Remember that the vertical velocity at the highest point of a parabola is zero. We can use that to find the time for the rock to travel upward.
Now let's find the time for the downward travel. We don't know the final velocity for the rock, but we CAN use the information we have been given to find the height it travels upward.
Remember, 



This means that our 

Add together the time for upward travel and downward travel to find the total flight time.
Example Question #1 : Linear Motion Calculations
Sam throws a 



What is the horizontal distance that the rock travels?
We first need to find the horizontal component of the initial velocity.
We can plug in the given values for the angle and initial velocity and solve.
The only force acting on the rock during flight is gravity; there are no forces in the horizontal direction, meaning that the horizontal velocity will remain constant. We can set up a simple equation to find the relationship between distance traveled and the velocity.
We know 
We need to solve for the time that the rock travels upward. We can then add the upward travel time to the downward travel time to find the total time in the air.
Remember that the vertical velocity at the highest point of a parabola is zero. We can use that to find the time for the rock to travel upward.
Now let's find the time for the downward travel. We don't know the final velocity for the rock, but we CAN use the information we have been given to find the height it travels upward.
Remember, 



This means that our 

Add together the time for upward travel and downward travel to find the total flight time.
Now that we've finally found our time, we can plug that back into the equation from the beginning of the problem, along with our horizontal velocity, to solve for the final distance.
Example Question #3 : Sat Subject Test In Physics
Sam throws a 



At what angle to the horizontal will the rock impact the ground?
The question gives the total initial velocity, but we will need to find the horizontal and vertical components.
To find the horizontal velocity we use the equation 
We can plug in the given values for the angle and initial velocity to solve.
We can find the vertical velocity using the equation 
The horizontal velocity will not change during flight because there are no forces in the horizontal direction. The vertical velocity, however, will be affected. We need to solve for the final vertical velocity, then combine the vertical and horizontal vectors to find the total final velocity.
We know that the rock is going to travel a net distance of 
Because the rock is traveling downward, our velocity will be negative: 
Now that we know our final velocities in both the horizontal and vertical directions, we can find the angle created between the two trajectories. The horizontal and vertical velocities can be compared using trigonometry.

Plug in our values and solve for the angle.
Example Question #1 : Sat Subject Test In Physics
If air resistance is negligible, 8 seconds after it is released, what would be the velocity of a stone dropped from a helicopter that has a horizontal velocity of 60 meters per second?
We are looking for total velocity, which in this case has both a horizontal and vertical component.
Because the helicopter is flying horizontally we know
We can assume that this takes place near the surface of the earth so
We can plug this into the equation:
Next we must find the horizontal velocity. Because there are no additional forces, the horizontal velocity is the same as the initial horizontal velocity of the helicopter, so:
Next we must use vector addition to add the horizontal and vertical components of velocity. Because this horizontal and vertical velocities are perpendicular the sum will be the hypotenuse of a right triangle:

Example Question #31 : Calculating Momentum
A 

The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 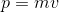
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Even though the ball is bouncing back at the same "speed" its velocity will now be negative, as it is moving in the opposite direction. Using this understanding we can solve for the force in our equation.
Our answer is negative because the force is moving the ball in the OPPOSITE direction from the way it was originally heading.
Example Question #151 : High School Physics
An egg falls from a nest in a tree that is 

More information is needed to solve
The important thing to recognize here is that the amount of time the egg is falling will be equal to the amount of time the girl is running.
Our first step will be to find the time that the egg is in the air.
We know it starts from rest 

Use the given values in the formula to solve for the time.
Now that we have the time, we can use it to find the speed of the girl. Her speed will be determined by the distance she travels in this amount of time.
Use our values for her distance and the time to solve for her velocity.
Example Question #1 : Kinematics Equations
A ball is dropped from the roof a building that is 
We can solve this problem using the kinematics equations. Note that the initial velocity will be zero, since the ball is dropped, and the acceleration will be equal to the acceleration of gravity.
This can be simplified, since the initial velocity is zero.
Use the given value for the distance (the height of the building) and the acceleration of gravity to solve for the time.
Certified Tutor
Certified Tutor
All SAT II Physics Resources