All SAT II Math II Resources
Example Questions
Example Question #11 : Trigonometry
A triangle has sides that measure 10, 12, and 16. What is the greatest measure of any of its angles (nearest tenth of a degree)?
We are seeking the measure of the angle opposite the side of greatest length, 16.
We can use the Law of Cosines, setting 

Example Question #1 : Law Of Cosines
A triangle has sides that measure 15, 17, and 30. What is the least measure of any of its angles (nearest tenth of a degree)?
We are seeking the measure of the angle opposite the side of least length, 15.
We can use the Law of Cosines, setting 

Example Question #2 : Law Of Cosines
Given :

Which of the following whole numbers is closest to 
Apply the Law of Cosines
setting 

Of the five choices, 27 comes closest.
Example Question #4 : Law Of Cosines
Given :

Evaluate 
The correct answer is not given among the other responses.
Apply the Law of Cosines
setting 

Example Question #1 : Law Of Cosines
In 
Evaluate the length of 
The figure referenced is below:
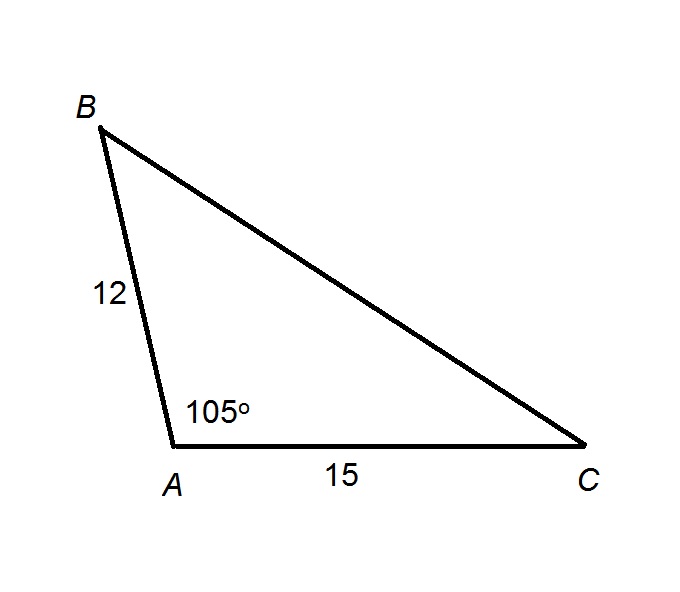
By the Law of Cosines, given the lengths 



Substituting 



Taking the square root of both sides:
Certified Tutor
All SAT II Math II Resources





























































