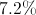Single-Variable Algebra

Help Questions

SAT Math › Single-Variable Algebra

Questions 1 - 10

Simplify the expression.

$\small \frac{(x^2y^2)(x^3y^4z)}{x^4y^3z^4}$

$\small \frac{xy^3}{z^3}$

$\small \frac{x^2y^5}{z^3}$

$\small \frac{z^3}{x^2y^5}$

$\small \frac{z^3}{xy^3}$

Explanation

$\small \frac{(x^2y^2)(x^3y^4z)}{x^4y^3z^4}$

Because we are only multiplying terms in the numerator, we can disregard the parentheses.

$\small \frac{(x^2y^2)(x^3y^4z)}{x^4y^3z^4}=\frac{x^2y^2x^3y^4z}{x^4y^3z^4}$

To combine like terms in the numerator, we add their exponents.

$\small \frac{x^5y^6z}{x^4y^3z^4}$

To combine like terms between the numerator and denominator, subtract the denominator exponent from the numerator exponent.

$x^{5-4}y^{6-3}z^{1-4}=xy^3z^{-3}$

Remember that any negative exponents stay in the denominator.

$\frac{xy^3}{z^3}$

If Bob fills a bucket with 9 logs that weigh 1.22 pounds each and the total weight of the bucket and logs 13.3 pounds, what percentage of the total weight is the bucket?

17.44%

.1744%

2.32%

18.60%

15.9%

Explanation

This question involves muliple steps to attain the correct answer.

To solve for the weight of the bucket (we will let 'x' represent this) the following equation can be set up:

To isolate x, subtract 9 * 1.22 (which is equal to 10.98) from both sides. We find x to be equal to 2.32.

The question asks us for the percentage of the total weight, so to find this, we must divide 2.32 by the total weight and multiple our answer by 100.

$\frac{2.32}{13.3}*100 = 17.44$

Rounded to two decimal points of accuracy, the final answer is 17.44%.

What is the solution set for ?

$-1\leq x \leq 6$

Explanation

Start by finding the roots of the equation by changing the inequality to an equal sign.

Now, make a number line with the two roots:

Pick a number less than and plug it into the inequality to see if it holds.

For ,

is clearly not true. The solution set cannot be .

Next, pick a number between $-1\text{ and }6$ .

For ,

is true so the solution set must include .

Finally, pick a number greater than .

For ,

is clearly not the so the solution set cannot be .

Thus, the solution set for this inequality is .

What is the solution set for ?

$-1\leq x \leq 6$

Explanation

Start by finding the roots of the equation by changing the inequality to an equal sign.

Now, make a number line with the two roots:

Pick a number less than and plug it into the inequality to see if it holds.

For ,

is clearly not true. The solution set cannot be .

Next, pick a number between $-1\text{ and }6$ .

For ,

is true so the solution set must include .

Finally, pick a number greater than .

For ,

is clearly not the so the solution set cannot be .

Thus, the solution set for this inequality is .

Simplify the expression.

$\small \frac{(x^2y^2)(x^3y^4z)}{x^4y^3z^4}$

$\small \frac{xy^3}{z^3}$

$\small \frac{x^2y^5}{z^3}$

$\small \frac{z^3}{x^2y^5}$

$\small \frac{z^3}{xy^3}$

Explanation

$\small \frac{(x^2y^2)(x^3y^4z)}{x^4y^3z^4}$

Because we are only multiplying terms in the numerator, we can disregard the parentheses.

$\small \frac{(x^2y^2)(x^3y^4z)}{x^4y^3z^4}=\frac{x^2y^2x^3y^4z}{x^4y^3z^4}$

To combine like terms in the numerator, we add their exponents.

$\small \frac{x^5y^6z}{x^4y^3z^4}$

To combine like terms between the numerator and denominator, subtract the denominator exponent from the numerator exponent.

$x^{5-4}y^{6-3}z^{1-4}=xy^3z^{-3}$

Remember that any negative exponents stay in the denominator.

$\frac{xy^3}{z^3}$

If Bob fills a bucket with 9 logs that weigh 1.22 pounds each and the total weight of the bucket and logs 13.3 pounds, what percentage of the total weight is the bucket?

17.44%

.1744%

2.32%

18.60%

15.9%

Explanation

This question involves muliple steps to attain the correct answer.

To solve for the weight of the bucket (we will let 'x' represent this) the following equation can be set up:

To isolate x, subtract 9 * 1.22 (which is equal to 10.98) from both sides. We find x to be equal to 2.32.

The question asks us for the percentage of the total weight, so to find this, we must divide 2.32 by the total weight and multiple our answer by 100.

$\frac{2.32}{13.3}*100 = 17.44$

Rounded to two decimal points of accuracy, the final answer is 17.44%.

Multiply the expressions:

$\small (x^{2} - 2x + 7) (x^{2} - 2x - 7)$

$\small x^{4}-4x^{3}+4x^2-49$

$\small \small x^{4}-4x^{3}+4x^2+49$

$\small \small \small x^{4}-4x^{3}-4x^2-49$

$\small \small \small \small \small x^{4}+4x^{3}-4x^2+49$

$\small \small \small \small x^{4}+4x^{3}-4x^2-49$

Explanation

You can look at this as the sum of two expressions multiplied by the difference of the same two expressions. Use the pattern

$\small (A+B)(A-B) = (A^{2}-B^{2})$ ,

where $\small A = x^{2} - 2x$ and $\small B = 7$ .

$\small \small \small (x^{2} - 2x + 7) (x^{2} - 2x - 7) = (x^{2} - 2x )^{2} - 7^{2} = (x^{2} - 2x )^{2} - 49$

To find $\small (x^{2} - 2x )^{2}$ , you use the formula for perfect squares:

$\small (A-B)^{2} = (A^{2}-2AB+B^{2})$ ,

where $\small \small A = x^{2}$ and $\small B = 2x$ .

$\small \small \small (x^{2}-2x)^{2} = ((x^{2})^{2}-2x^{2}(2x)+(2x)^{2}) = x^{4}-4x^{3}+4x^2$

Substituting above, the final answer is $\small x^{4}-4x^{3}+4x^2-49$ .

Give the set of all real solutions of the equation $2x^{4} - 13x^{2} +21 = 0$ .

$\left { - \frac{\sqrt{14}}{2}, - \sqrt{3}, \sqrt{3} ,\frac{ \sqrt{14}}{2} \right }$

$\left { \sqrt{3} ,\frac{ \sqrt{14}}{2} \right }$

$\left { - \sqrt{3}, \sqrt{3} \right }$

$\left { - \frac{\sqrt{14}}{2}, \frac{ \sqrt{14}}{2} \right }$

The equation has no real solution.

Explanation

Set $y = x^{2}$ . Then $x^{4 } = \left (x^{2} \right )^{2} = y ^{2}$ .

$2x^{4} - 13x^{2} +21 = 0$ can be rewritten as

$2 \left (x^{2} \right )^{2} - 13x^{2} +21 = 0$

Substituting $y^{2}$ for $x^{4 }$ and for $x^{2}$ , the equation becomes

$2 y^{2} - 13y +21 = 0$ ,

a quadratic equation in .

This can be solved using the method. We are looking for two integers whose sum is and whose product is . Through some trial and error, the integers are found to be and , so the above equation can be rewritten, and solved using grouping, as

$2 y^{2} - 7y - 6y +21 = 0$

$(2 y^{2} - 7y )- (6y -21 )= 0$

By the Zero Product Principle, one of these factors is equal to zero:

Either:

Substituting $x^{2}$ back for :

$x^{2} = 3$

Taking the positive and negative square roots of both sides:

$x = \pm \sqrt{3}$ .

Or:

$\frac{2y}{2} =\frac{ 7}{2}$

$y =\frac{ 7}{2}$

Substituting back:

$x^{2} =\frac{ 7}{2}$

Taking the positive and negative square roots of both sides, and applying the Quotient of Radicals property, then simplifying by rationalizing the denominator:

$x =\pm \sqrt{\frac{ 7}{2}} = \pm \frac{\sqrt{7}}{\sqrt{2}} = \pm \frac{\sqrt{7} \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2} } =\pm \frac{\sqrt{14}}{2}$

The solution set is $\left { - \frac{\sqrt{14}}{2}, - \sqrt{3}, \sqrt{3} ,\frac{ \sqrt{14}}{2} \right }$ .

Solve the inequality: $2x-26\leq 22$

$x\leq 24$

$x\geq-2$

$x\geq24$

Explanation

Add 26 on both sides.

$2x-26+26\leq 22+26$

$2x\leq 48$

Divide by two on both sides.

$\frac{2x}{2}\leq \frac{48}{2}$

The answer is: $x\leq 24$

If Jane buys four cans of soda at \$1.56 each and pays \$6.93 total, what is the percentage of the sales tax?

Explanation

How to calculate the amount of sales tax?

Convert tax percentage into a decimal by moving the decimal point two spaces to the left.
Multiple the pre-tax value by the newly calculated decimal value in order to find the cost of the sales tax.
Add the sales tax value to the pre-tax value to calculate the total cost.

Calculating sales tax at time of purchase:

In order to calculate the sales tax of an item, we need to first multiply the pre-tax cost of the item by the sales tax percentage after it has been converted into a decimal. Once the sales tax has been calculated it needs to be added to the pre-tax value in order to find the total cost of the item. Let's start by working with an example. If a magazine costs \$2.35 and has a 6% sales tax, then what is the total cost of the item. First, we need to convert the sales tax percentage into a decimal by moving the point two spaces to the left.

$6% \rightarrow 0.06$

Now, we need to multiply the pre-tax cost of this item by this value in order to calculate the sales tax cost.

$\textup{Sales tax}=0.06\times\$2.35$

$\textup{Sales tax}=\$0.141$

Round to two decimal places since our total is in dollars and cents.

$\textup{Sales tax}=\$0.14$

Last, add this value to the pre-tax value of the item to find the total cost.

$\textup{Total cost}=\textup{Pre-tax value}+\textup{Sales tax}$

$\textup{Total cost}=$2.35+$0.14$

$\textup{Total cost}=\$2.49$

Calculating the sales tax percentage of a total:

If we are given the total cost of an item or group of items and the pre-tax cost of the good(s), then we can calculate the sales tax percentage of the total cost. First, we need to subtract the pre-tax value from the total cost of the purchase. Next, we need to create a ratio of the sales tax to the pre-tax cost off the items. Last, we need to create a proportion where the pre-tax cost is related to 100% and solve for the percentage of the sales tax. Let's start by working through an example. If a person pays \$245.64 for groceries that cost \$220.00 pre tax, then what is the sales tax percentage for the items.

First, subtract the pre-tax value from the total cost of the items to find the sales tax cost.

$\textup{Sales tax}=\textup{Total cost}-\textup{Pre-tax value}$

$\textup{Sales tax}=\$245.64-\$220.00$

$\textup{Sales tax}=\$25.64$

Next, create a ratio of the sales tax to the pre-tax cost of the items.

$\frac{\textup{Sales tax}}{\ \textup{Pre-tax value}} = \frac{$25.64}{$220.00}$

Last, create a proportion where the pre-tax value is proportional to 100% and solve for the percentage of sales tax.

$\frac{$25.64}{$220.00}=\frac{\textup{Sales tax percentage}}{100%}$

Cross multiply and solve.

$\$220.00\times\textup{Sales tax percentage}=\$25.64\times 100%$

$\$220.00\times\textup{Sales tax percentage}=\$2564.00$

Isolate the sales tax percentage to the left side of the equation by dividing each side by the pre-tax value.

$\frac{\$220.00\times\textup{Sales tax percentage}}{\$220.00}=\frac{$2564.00}{$220.00}$

$\textup{Sales tax percentage}=11.6545455%$

Round to two decimal places since our answer is in dollars and cents.

$\textup{Sales tax percentage}=11.65%$

Last, we can check this answer by calculating the sales tax percentage of the total as seen previously.

First, we need to convert the sales tax percentage into a decimal by moving the point two spaces to the left.

$11.6545455% \rightarrow 0.116545455$

Now, we need to multiply the pre-tax cost of this item by this value in order to calculate the sales tax cost.

$\textup{Sales tax}=0.116545455\times\$220.00$

$\textup{Sales tax}=\$25.6400001$

Round to two decimal places since our total is in dollars and cents.

$\textup{Sales tax}=\$25.64$

Last, add this value to the pre-tax value of the item to find the total cost.

$\textup{Total cost}=\textup{Pre-tax value}+\textup{Sales tax}$

$\textup{Total cost}=\$220.00+\$25.64$

$\textup{Total cost}=\$245.64$

Our answers check out; therefore they are correct. Now, let's use this information to solve the given problem.

Solution:

If each soda cost \$1.56 and Jane bought four, the total for the sodas was:

$1.56\cdot 4=6.24$

And she paid \$6.93

$\frac{6.93}{6.24}=1.11$

The sales tax was 11%.

Page 1 of 42

Return to subject

AI TutorYour personal study buddy

Question of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games