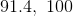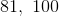All SAT II Math I Resources
Example Questions
Example Question #1 : Median
What is the median of 13, 12, 22, 7, 7, 8, 13, 27, 30?
The median is middle number of a set, when the numbers are arranged in order from least to greatest.
In our case we re arrange our numbers in the following fashion:
7, 7, 8, 12, 13, 13, 22, 27, 30
The middle number in our case is the 5th entry.
Therefore, the median is 13
Example Question #1 : Median
What is the median of 3, 7, 6, 11, 14, 9?
The median is the middle number in a set of numbers when arranged in order from least to greatest.
In our case we get
3, 6, 7, 9, 11, 14
This set has two middle numbers 7 and 9. From here we need to find the average between these two numbers to find our median:
Example Question #3 : Median
What's the median?
Median is to find the middle number arranging from smallest to greatest. So we have 



Example Question #2 : Median
If the lowest value in a set was decreased and the highest value in the same set was increased, how would that affect the median?
It would increase
It would stay the same
It would decrease
Not enough information to give an adequate answer
It would stay the same
The median is the middle number of a set. If the same amount of values are used and the actual middle number is not changed, the median of the set will not change. Changing the actual values of the two extremes did not change them position wise in the set when placed in value order.
Example Question #1 : How To Find The Median For A Set Of Data
Let 
Find the median of the set.
The median is the middle value of the set in increasing order.
In this set of 8 (or any even number) entries, the median is the mean of the two middle entries of the set in increasing order
or
Example Question #1 : Median
Consider the following test scores from a typical high school class with 
The mean of this data set is_________, and the mode of this data set is _______.
The mean is just the average of all the test scores, which is found by adding up the scores and dividing by the number of scores (



Example Question #203 : Data Properties
What is the median of the first 20 even numbers?
Cannot be calculated
Let's think of this list of numbers:
2, 4, 6, ...
Where does it end? The first 5 even numbers goes to 10. That means that the last number in the first 20 will be the number 40. So the question is, "Where is the middle?" Well, this is an even number of values, so there is no actual middle. What we have to do, then is find the 10th and the 11th numbers and take their average. The 10th number is easy, based on what we just said. If the 5th is 10, then the 10th is 20. The 11th will just be two more than that, namely 22. To calculate the median, we just have to find the average of those two numbers:
If you prefer to write out the full list:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40
Example Question #1 : Median
What is the median of the first ten prime numbers?
To answer this question, you need to know the first ten prime numbers! Remember, prime numbers are all of the integers that are divisible only by themselves and by 1. They do not include 1. So, our list is:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
The median is the "middle value." There is no proper "middle" since we have an even number of values. We need to take the 5th and the 6th elements (the middle two values) and average them. The 5th term is 11 and the 6th is 13; therefore, the median is:
Example Question #691 : Sat Subject Test In Math I
There is a table of flowers prepared for sale. Twelve flowers are 


The easiest way to do this is first to find the total number of flowers:
Now, the median element is the "middle" term. To find the middle, you can divide 21 by 2:
Since you have an odd number of elements, you unsurprisingly get a fraction. This means that there 10 items to the left of the median and 10 to its right. The 11th term is your median. Now, your group of flowers looks like this:
1-12: 10 inches
13-17: 12 inches
18-21: 15 inches
The 11th item is going to be in that first group, meaning that the median is 10 inches.
If you prefer to write out all of the terms, it will be:
10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 12, 12, 12, 12, 12, 15, 15, 15, 15
Example Question #2 : Median
There are 1000 magical beanstalks planted in a row. Each stalk is 10 feet taller than the one before it. The smallest stalk is 10 feet tall. What is the median height of the stalks?
No median can be calculated
The first thing to do is figure out which stalk is in the "middle." Since there are an even number of stalks, there is no exact middle; there are 500 on one side and 500 on the other. This means that the 500th and the 501st are the median. These will have to be averaged.
Now, we need to determine the height of these two stalks. Consider the pattern given:
1st stalk: 10 feet
2nd stalk: 20 feet
3rd stalk: 30 feet
4th stalk: 40 feet
You should see the pattern that emerges for this problem. Each stalk is 10 times that stalk's place in the row. This means that the 500th stalk will be:
The 501st stalk will be:
The average of these two numbers is:
5005 feet is the median.
All SAT II Math I Resources