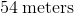How to find the perimeter of a rectangle
Help Questions
PSAT Math › How to find the perimeter of a rectangle

Note: Figure NOT drawn to scale
Refer to the above figure, which shows a square garden (in green) surrounded by a dirt path (in orange) eight feet wide throughout. What is the perimeter of the garden?
Explanation
The inner square, which represents the garden, has sidelength 


Note: Figure NOT drawn to scale
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in orange). The dirt path is seven feet wide throughout. Which of the following polynomials gives the perimeter of the garden in feet?
Explanation
The length of the garden, in feet, is 

The width of the garden, in feet, is 

The perimeter, in feet, is twice the sum of the two:
Farmer Dave has a rectangular field that is 50 yards wide and 40 yards long. He wants to enclose the field with a wire fence. How much wire does Farmer Dave need?
180 yards
200 yards
160 yards
170 yards
210 yards
Explanation
To solve this problem, find the perimeter of the rectangle. There are two sides that each measure 50 yards and two sides that each measure 40 yards. Together these four sides measure 180 yards.
A rectangular garden has an area of 

Explanation
We define the variables as 

We substitute these values into the equation for the area of a rectangle and get 

Lengths cannot be negative, so the only correct answer is 


Therefore, 
A rectangle has a width of 2_x_. If the length is five more than 150% of the width, what is the perimeter of the rectangle?
10(x + 1)
5_x_ + 5
5_x_ + 10
6_x_2 + 10_x_
6_x_2 + 5
Explanation
Given that w = 2_x_ and l = 1.5_w_ + 5, a substitution will show that l = 1.5(2_x_) + 5 = 3_x_ + 5.
P = 2_w_ + 2_l_ = 2(2_x_) + 2(3_x_ + 5) = 4_x_ + 6_x_ + 10 = 10_x_ + 10 = 10(x + 1)