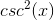All Precalculus Resources
Example Questions
Example Question #1 : Sum And Difference Identities For Tangent
According to the trigonometric identities,
The trigonometric identity 
Some other identities that are important to know are:
Example Question #1 : Trigonometric Identities
Use the sum or difference identity to find the exact value:
Again, here we break up the 165 into 

Example Question #1 : Sum And Difference Identities For Sine
Is the following equation an identity?
No it is not an identity.
It cannot be determined from the given information.
Yes it is an identity.
No it is not an identity.
and so this is again not an identity
Example Question #2 : Sum And Difference Identities For Sine
Is the following equation an identity? 
No it is not an identity
Yes it is an identity
The question cannot be answered based on the information provided.
Example Question #1 : Sum And Difference Identities For Cosine
Use the sum or difference identity to find the exact value:
Example Question #1 : Sum And Difference Identities For Cosine
Is the following equation an identity?
No it is not an identity.
Yes it is an identity.
It cannot be determined from the given information.
No it is not an identity.
and due to this inequality, this is not an identity
Example Question #212 : Pre Calculus
Use the sum or difference identity to find the exact value:
Using the identity, we can break up the 



Example Question #2 : Sum And Difference Identities For Cosine
The answer cannot be determined from the information provided.
Yes it is an identity
No it is not an identity
Example Question #214 : Pre Calculus
Use the sum or difference identity to find the exact value of 
Here we break up the 



Example Question #1 : Trigonometric Identities
Use trigonometric identities to solve the following equation for 
Use the trigonometric identities to switch sec into terms of tan:
hence,
So we have 
Therefore the solution is 
Certified Tutor
Certified Tutor
All Precalculus Resources