All Pre-Algebra Resources
Example Questions
Example Question #1 : Geometry
Betty needs to buy carpeting to cover her entire bedroom floor, which is 12 ft. long and 8 ft. wide. How much carpeting does she need to buy?
Remember to use the formula below to find area:
Since Betty needs carpeting to cover her floor, this problem asks you to find the area. This means you need to multiply length and width to find the area, which is given in square feet, since each foot of carpeting is not only one foot long, but also one foot wide (a square).
Step 1: plug in the numbers for length and width
Step 2: solve
Example Question #2 : Geometry

The rectangle in the above figure has length 20 and height 10. What is the area of the red region?
Insufficient information is given to determine the area.
The red region is formed by removing a triangle from a rectangle.
The rectangle measures 20 by 10, and, subsequently, has area

The triangle has base 10. Its height is the radius of the circle, which is 5, so its area is

The difference between the areas, which is the area of the red region, is 
Example Question #3 : Geometry

The rectangle in the above figure has length 20 and height 10. What is the area of the red region?
Insufficient information is given to determine the area.
The red region is a composite of two figures:
One is a rectangle measuring 20 by 10, which, subsequently, has area

The other is a triangle with base 10. Its height is the radius of the circle, which is 5, so its area is

The sum of the areas, which is the area of the red region, is 
Example Question #4 : Geometry
Thompson High School wants to buy artificial turf for their practice soccer field. The field is 150 ft by 100 ft. How much turf should they buy?


Recall, the area of a rectangle = length x width
Next, plug in the two values given in the problem
Example Question #3 : Geometry
Judy needs to buy a glass table cover for a dinner party, which is 8 ft. long and 3 ft. wide. How much glass does she need to buy?
Explanation:
Remember to use the formula below to find area:
Since Judy needs enough glass to cover the whole table, this problem asks you to find the area. This means you need to multiply length and width to find the area, which is given in square feet, since each foot of glass is not only one foot long, but also one foot wide (a square).
Step 1: Plug in the numbers for the length and width
Step 2: Solve
Example Question #1 : Geometry
Jessica's blanket is 12 square feet. Lisa has a blanket that is half the size of Jessica's blanket. Which of the following are possible dimensions of Lisa's blanket?
The area of a rectangle if found by multiplying the length times the width. Here, we know that Lisa's blanket is half the area of Jessica's blanket. Since Jessica's blanket is 12 square feet, that means that Lisa's blanket must be 6 square feet.
The only length and width values that give us 6 square feet when multiplied by one another are 3 feet by 2 feet. This is therefore the correct answer.
Example Question #6 : Geometry
Jon built a new garden with two sides equalling 

In order to do this problem you must imagine the garden as a rectangle with sides of 



The formula for area of a rectangle is 
In our case the length is 10 and the width is 15. To find the area of a rectangle you must multiply 

Example Question #322 : Ssat Middle Level Quantitative (Math)
The area of a rectangle can be found by multiplying the length by the width.
Example Question #9 : Area Of A Rectangle Or Square
A square has a perimeter of 
A square with a perimeter of 









Example Question #10 : Area Of A Rectangle Or Square
A square has a perimeter of 
Not enough information given to solve.
A square has a perimeter of 


The area of a square is length x width, and in this case 

All Pre-Algebra Resources


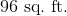


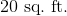


































 . Solve for
. Solve for  .
.























